The moment of inertia of a solid cylinder of density ρ, radius of base r, and height h about an axis passing through its centre of mass and parallel to length is
π2r4hρ
π2r2hρ
π2r3hρ
π2rhρ
To find the moment of inertia of a solid cylinder about an axis passing through its center of mass and parallel to its length, we can follow these steps:
Step 1: Understand the Geometry of the Cylinder
We have a solid cylinder with:
- Density = ρ
- Radius = r
- Height = h
Step 2: Define the Moment of Inertia
The moment of inertia (I) about an axis is given by the integral of the mass elements (dm) times the square of their distance (r²) from the axis of rotation:
I=∫r2dm
Step 3: Express dm in Terms of Density and Volume
The mass element (dm) can be expressed in terms of the density (ρ) and the volume (dV) of an infinitesimally thin cylindrical shell:
dm=ρdV
Step 4: Calculate the Volume Element dV
For a thin cylindrical shell of thickness dr, the volume element dV can be calculated as:
dV=Area×Height=(2πrdr)×h
Thus,
dV=2πrhdr
Step 5: Substitute dm into the Moment of Inertia Formula
Now substituting for dm in the moment of inertia equation:
I=∫r2dm=∫r2(ρdV)=∫r2(ρ⋅2πrhdr)
Step 6: Set Up the Integral
Now we can set up the integral:
I=∫r0(r2)⋅(2πρhr)dr
This simplifies to:
I=2πρh∫r0r3dr
Step 7: Evaluate the Integral
Now we evaluate the integral:
∫r0r3dr=(r44)r0=r44
Step 8: Substitute Back into the Moment of Inertia Formula
Substituting back, we get:
I=2πρh⋅r44=2πρhr44=πρhr42
Final Answer
Thus, the moment of inertia of the solid cylinder about an axis passing through its center of mass and parallel to its length is:
I=πρhr42
We have a solid cylinder with:
- Density = ρ
- Radius = r
- Height = h
The moment of inertia (I) about an axis is given by the integral of the mass elements (dm) times the square of their distance (r²) from the axis of rotation:
I=∫r2dm
The mass element (dm) can be expressed in terms of the density (ρ) and the volume (dV) of an infinitesimally thin cylindrical shell:
dm=ρdV
For a thin cylindrical shell of thickness dr, the volume element dV can be calculated as:
dV=Area×Height=(2πrdr)×h
Thus,
dV=2πrhdr
Now substituting for dm in the moment of inertia equation:
I=∫r2dm=∫r2(ρdV)=∫r2(ρ⋅2πrhdr)
Now we can set up the integral:
I=∫r0(r2)⋅(2πρhr)dr
This simplifies to:
I=2πρh∫r0r3dr
Now we evaluate the integral:
∫r0r3dr=(r44)r0=r44
Substituting back, we get:
I=2πρh⋅r44=2πρhr44=πρhr42
Thus, the moment of inertia of the solid cylinder about an axis passing through its center of mass and parallel to its length is:
I=πρhr42
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)
60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
The moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View SolutionThe radius of gyration of a uniform rod of length L about an axis passing through its centre of mass is
View SolutionThe moment of inertia of a solid cylinder about its own axis is the same as its moment of inertia about an axis passing through its centre of gravity and perpendicular to its length. The relation between its length L and radius R is :
View SolutionFind the moment of inertia of a cylinder of mass M, radius R and length L about an axis passing through its centre and perpendicular to its symmetry axis. Do this by integrating an elemental disc along the length of the cylinder.
View SolutionThe moment of inertia of a uniform semicircular wire of mass m and radius r, about an axis passing through its centre of mass and perpendicular to its plane is mr2(−kπ2). Find the value of k.
View SolutionWhat is the moment of inertia of a solid sphere of density ρ and radius R about its diameter ?
View SolutionMatch the Moment of inertia of a solid cylinder of mass m, radius R and length l along various axis as shown in figure.
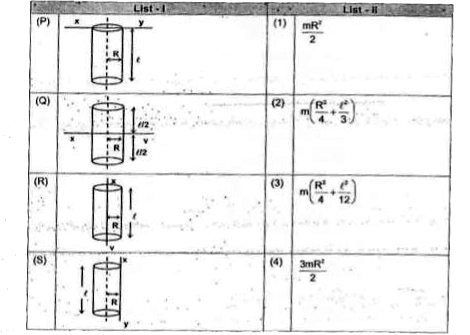
View SolutionWhat is the moment of inertia of solid sphere of density ρ and radius R about its diameter ?
View SolutionWhat is moment of inertia of a cylinder of radius r, along its height?
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View Solution
