The figure represents two identical slits in a Young’s double slit experiment. The width of each slit is b and distance between the centres of the two slits is d. Consider a point P on the screen that is close to centre of the screen. Δxt represents the optical path difference to point P from the top edges of the two slits and Δxb represents the optical path difference to P from the bottom edges of the two slits. FindΔxb–Δxt.
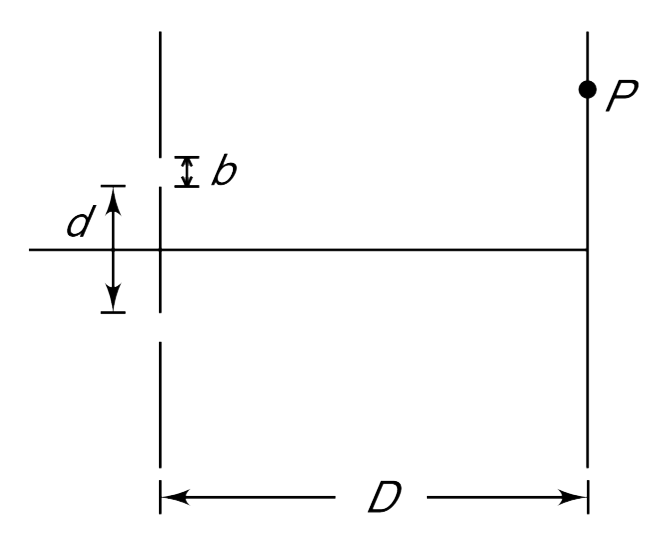
The figure represents two identical slits in a Young’s double slit experiment. The width of each slit is b and distance between the centres of the two slits is d. Consider a point P on the screen that is close to centre of the screen. Delta x(t) represents the optical path difference to point P from the top edges of the two slits and Delta x(b) represents the optical path difference to P from the bottom edges of the two slits. Find Delta x(b) – Delta x(t). It is given that D gtgt d.
It is given that D>>d.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:dbD

Updated on:21/07/2023
|
Answer

Step by step video, text & image solution for The figure represents two identical slits in a Young’s double slit experiment. The width of each slit is b and distance between the centres of the two slits is d. Consider a point P on the screen that is close to centre of the screen. Delta x_(t) represents the optical path difference to point P from the top edges of the two slits and Delta x_(b) represents the optical path difference to P from the bottom edges of the two slits. Find Delta x_(b) – Delta x_(t). It is given that D gtgt d. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12PHYSICSWAVE OPTICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • If the two slits in Young's double slit experiment are of unequal width, then

    Athe bright fringes will have unequal spacing.
    Bthe bright fringes will have unequal brightness
    Cthe fringes do not appear
    Dthe dark fringes are not perfectly dark.

  • In a Young's double slit experiment, the central point on the screen is

    ABright
    BDark
    CFirst bright and then dark
    DFirst dark and then bright

  • In Young’s double slit experiment, the wavelength of the light used is doubled and distance between two slits is half of initial distance, the resultant fringe width becomes

    A2 times
    B3 times
    C4 times
    D1/2 times