If the depth d to which a bullet of kinetic energy K can penetrate int

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS
866 Videos
TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- B
1 Videos
SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos

Knowledge Check

The time period of oscillation of a body is given by $T = 2 π \sqrt{\frac{m g A}{K}}$
K: Represents the kinetic energy, m mass, g acceleration due to gravity and A is unknown If $[A] = M^{x} L^{y} T^{z}$ , then what is the value of x+y+z?
A3
B2
C1
D5
When the temperature is increased, heat is supplied which increases the kinetic energy of the reacting molecules. This shall increase the number of collisions and ultimately the rate of reaction shall be enhanced. Arrhenius suggested a equation which describes $K$ as a function of temperature, i.e.
$k = A e_{a}^{- E_{a} / R T}$
where
$k =$ rate constant
$A =$ a constant (frequency factor)
$E_{a} =$ energy of activation
${log}_{10} k = {log}_{10} A - \frac{E_{a}}{2.303 R} [\frac{1}{R}]$
$Y = C + M X$
It is the equation of straight line with negative slope. On plotting ${log}_{10} k$ against $[\frac{1}{T}]$ we get a straight line as shown below :

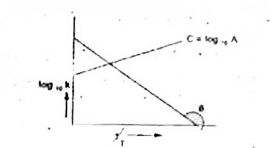
The slope gives activation energy and intercept gives frequency factor.
Also $log . \frac{k_{2}}{k_{1}} = \frac{E_{a}}{2.303} [\frac{T_{2} - T_{1}}{T_{1} T_{2}}]$
The rate of certain reaction increases by $2.5$ times when the temperature is raised from $300 K$ to $310 K$ . If $k$ is the rate constant at $300 K$ then rate constant at $310 K$ will be equal to
A $k$
B $2 k$
C $2.5 k$
D $13 k$
A student forgot Newton's formula for speed of sound but the knows there speed (v), pressure (p) and density (d) in the formula. He then start using dimensional analysis method to find the actual relation.
$υ = k p^{x} d^{y}$
Where k is a dimensionless constant. On the basis of above passage answer the following questions:
The value of y is :
A1
B $\frac{1}{2}$
C $- \frac{1}{2}$
D2

If the depth d to which a bullet of kinetic energy K can penetrate into a human body of modulus of electicity E, using the method of dimension, establish a relation between d, K and E . If $K = c d^{x} E^{y}$ , fill x+y in OMR sheet. Modulus of elasticity =Force/Area , $\times \frac{l}{Δ l}$

The correct Answer is: $0004$

$K = c d^{x} E^{y}$
$M L^{2} T^{- 2} = L^{X} {[M L^{- 1} T^{- 2}]}^{Y}$
$- 2 = - 2 y \Rightarrow y = 1$
$2 = x - y \Rightarrow x = 3 x + y = 4$

Topper's Solved these Questions

Similar Questions

Knowledge Check

The time period of oscillation of a body is given by $T = 2 π \sqrt{\frac{m g A}{K}}$
K: Represents the kinetic energy, m mass, g acceleration due to gravity and A is unknown If $[A] = M^{x} L^{y} T^{z}$ , then what is the value of x+y+z?

BANSAL-TEST PAPERS-PHYSICS PART- C

If the depth d to which a bullet of kinetic energy K can penetrate into a human body of modulus of electicity E, using the method of dimension, establish a relation between d, K and E . If K=cdxEy, fill x+y in OMR sheet. Modulus of elasticity =Force/Area ,×lΔl

The correct Answer is:0004

K=cdxEy ML2T−2=LX[ML−1T−2]Y −2=−2y ⇒y=1 2=x−y ⇒x=3 x+y=4

Topper's Solved these Questions

Similar Questions

Knowledge Check

The time period of oscillation of a body is given by T=2π√mgAK K: Represents the kinetic energy, m mass, g acceleration due to gravity and A is unknown If [A]=MxLyTz, then what is the value of x+y+z?

BANSAL-TEST PAPERS-PHYSICS PART- C

If the depth d to which a bullet of kinetic energy K can penetrate into a human body of modulus of electicity E, using the method of dimension, establish a relation between d, K and E . If $K = c d^{x} E^{y}$ , fill x+y in OMR sheet. Modulus of elasticity =Force/Area , $\times \frac{l}{Δ l}$

The correct Answer is: $0004$

$K = c d^{x} E^{y}$
$M L^{2} T^{- 2} = L^{X} {[M L^{- 1} T^{- 2}]}^{Y}$
$- 2 = - 2 y \Rightarrow y = 1$
$2 = x - y \Rightarrow x = 3 x + y = 4$

The time period of oscillation of a body is given by $T = 2 π \sqrt{\frac{m g A}{K}}$
K: Represents the kinetic energy, m mass, g acceleration due to gravity and A is unknown If $[A] = M^{x} L^{y} T^{z}$ , then what is the value of x+y+z?