A small particle starts moving from point P along the smooth inclined surface of circular cross section seen in figure (R=5m)

The different of height between the highest point of the trajectory and the point P is 6425m
The ratio of the kinetic energies at the highest point of the trajectory and the lowest point of the circular path is 64125.
The difference of height between the highest point of the trajectory and the point P is 3625m
The ratio of the total mechanical energies at the highest point of the trajectory and the lowest point of the circular path is 1.
The correct Answer is:ABD

mg×4=12mv2
v=√80
h=v2sin237∘2g=8020×925=3625m
ΔH=4−3625=6425m
mg×5=12mv21
vtop=vcosθ=√80×45
KtopKbottom=12m×80×1625mg×5=64125
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
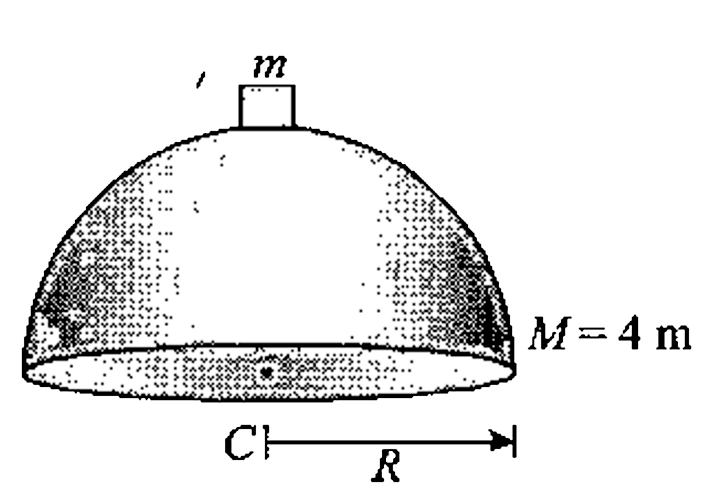
A small block of mass m starts sliding down from rest along the smooth surface of a fixed hollow hemisphere of same mass m. Find the distance of centre of mass of block and hemishere from centre of hemisphere C when block m separates from the surface of hemisphere.
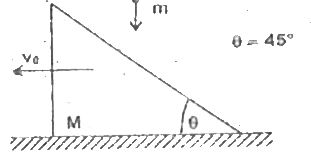
View SolutionA triangular wedge of mass M is moving with uniform velocity v0 along a smooth horizontal surface in the leftward direction. A particle of mass m falls from rest from height h onto the inclined face, colliding elastically with it. Find velocity of the ball and wedge after the impact taking M = 2m.
View Solution
Knowledge Check
A particle starts from rest from point P and follow a path PQ on the three smooth surfaces as shown in figures. If time taken by the particle in three cases are t1,t2 and t3 then
 At1>t2>t3Bt3>t2>t1Ct3>t1>t3Dt1=t2=t3
At1>t2>t3Bt3>t2>t1Ct3>t1>t3Dt1=t2=t3A particle of mass m initially at rest starts moving from point A on the surface of a fixed smooth hemisphere of radius r as shown. The particle looses its contact with hemisphere at point B.C is centre of the hemisphere. The equation relating θ and θ' is
 .A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'
.A3sinθ=2cosθ'B2sinθ=3cosθ'C3sinθ'=2cosθD2sinθ=3cosθ'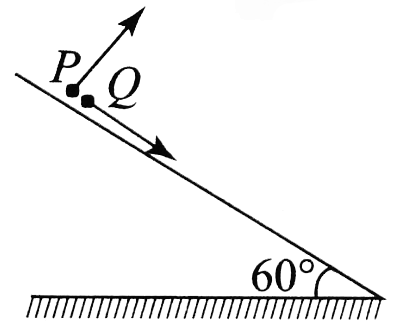
A particle P is projected from a point on the surface of smooth inclined plane (see figure). Simultaneously another particle Q is released on the smooth inclined plane from the same position. P and Q collide aftert=4. The speed of projection of P isA5msB10msC15msD20ms
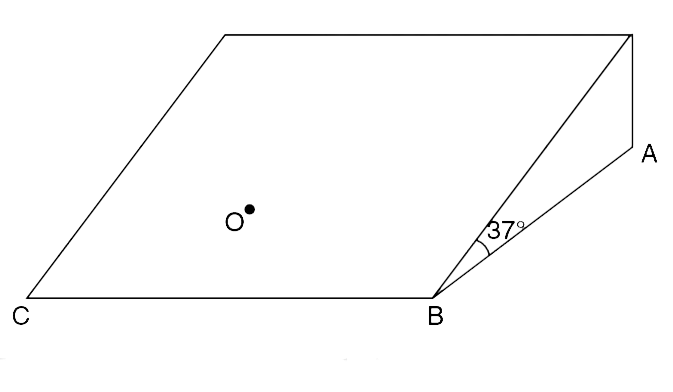
There is a large wedge placed on a horizontal surface with its incline face making an angle of 37∘ to the horizontal. A particle is projected in vertically upward direction with a velocity of u=6.5m/s from a point O on the inclined surface. At the instant the particle is projected, the wedge begins to move horizontally with a constant acceleration of a=4m/s2. At what distance from point O will the particle hit the incline surface if
(i) direction of a is along BC?
(ii) direction of a is along AB?
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
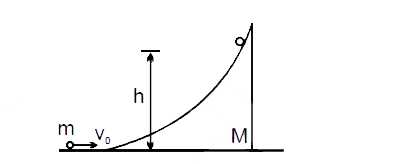
Identify the correct statement(s) related to the situation when the particle starts moving downward
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
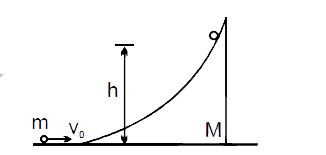
Choose the correct statement(s) related to particle m
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
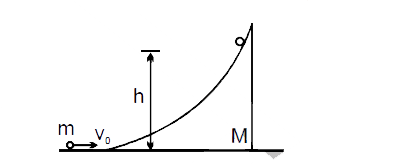
When the particle has risen to a height h on the wedge, then choose the correct alternative(s)
View SolutionA particle starts from point A moves along a straight line path with an acceleration given by a=p−qx where p, q are connected and x is distance from point A . The particle stops at point B. The maximum velocity of the particle is
View Solution
