A car starts with constant acceleration a=2m/s2 at t=0. two coins are released from the car at t=3 and t=4 . Each coin takes 1 second to fall on ground. Then the distance between the two coins will be (Assume coin sticks to the ground)
9m
7m
15 m
2m
The correct Answer is:1
To solve the problem, we need to analyze the motion of the car and the coins dropped from it. Let's break it down step by step.
Step 1: Calculate the velocity of the car at t = 3 seconds
The formula for velocity under constant acceleration is:
V=U+aT
Where:
- U=0 (initial velocity, since the car starts from rest)
- a=2m/s2 (constant acceleration)
- T=3s
Substituting the values:
V1=0+2×3=6m/s
Step 2: Calculate the velocity of the car at t = 4 seconds
Using the same formula:
V2=U+aT
Where:
- T=4s
Substituting the values:
V2=0+2×4=8m/s
Step 3: Determine the horizontal distance traveled by each coin after being dropped
When the first coin is dropped at t=3s, it has a horizontal velocity of 6m/s. It will fall for 1s before hitting the ground:
Distance traveled by Coin 1(S1)=velocity×time=6m/s×1s=6m
When the second coin is dropped at t=4s, it has a horizontal velocity of 8m/s and also falls for 1s:
Distance traveled by Coin 2(S2)=8m/s×1s=8m
Step 4: Calculate the distance traveled by the car between the two drops
The car is accelerating, so we can find the distance it travels between t=3s and t=4s using the formula:
S=V1⋅t+12at2
Where:
- V1=6m/s (initial velocity at t=3s)
- t=1s (time interval)
- a=2m/s2
Calculating the distance:
S=6⋅1+12⋅2⋅(1)2=6+1=7m
Step 5: Find the distance between the two coins
Now we can find the distance between the two coins. The first coin travels 6m from its drop point, and the second coin travels 8m from its drop point. The car itself moves 7m during the time between the drops.
The distance between the two coins is:
Distance=S2−S1+Distance traveled by car
Distance=8m−6m+7m=9m
Final Answer
The distance between the two coins when they hit the ground is 9 meters.
The formula for velocity under constant acceleration is:
V=U+aT
Where:
- U=0 (initial velocity, since the car starts from rest)
- a=2m/s2 (constant acceleration)
- T=3s
V1=0+2×3=6m/s
Using the same formula:
V2=U+aT
Where:
- T=4s
V2=0+2×4=8m/s
When the first coin is dropped at t=3s, it has a horizontal velocity of 6m/s. It will fall for 1s before hitting the ground:
Distance traveled by Coin 1(S1)=velocity×time=6m/s×1s=6m
Distance traveled by Coin 2(S2)=8m/s×1s=8m
The car is accelerating, so we can find the distance it travels between t=3s and t=4s using the formula:
S=V1⋅t+12at2
Where:
- V1=6m/s (initial velocity at t=3s)
- t=1s (time interval)
- a=2m/s2
S=6⋅1+12⋅2⋅(1)2=6+1=7m
Now we can find the distance between the two coins. The first coin travels 6m from its drop point, and the second coin travels 8m from its drop point. The car itself moves 7m during the time between the drops.
Distance=S2−S1+Distance traveled by car
Distance=8m−6m+7m=9m
The distance between the two coins when they hit the ground is 9 meters.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)32videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)3videos
TEST PAPERS
- BOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C4videos
TEST PAPERS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
There are two cars on a straight road, marked as x axis. Car A is travelling at a constant speed of VA=9m/s. Let the position of the Car A, at time t=0, be the origin. Another car B is L=40m ahead of car A at t=0 and starts moving at a constant acceleration of a=1m/s2 (at t = 0). Consider the length of the two cars to be negligible and treat them as point objects.

(a) Plot the position–time (x–t) graph for the two cars on the same graph. The two graphs intersect at two points. Draw conclusion from this.
(b) Determine the maximum lead that car A can have.View SolutionA balloon starts rising upwards with constant acceleration a and afrer time t0, second, a packet is dropped from it which reaches the ground aftre t seconds of dropping . Derermine the value of t
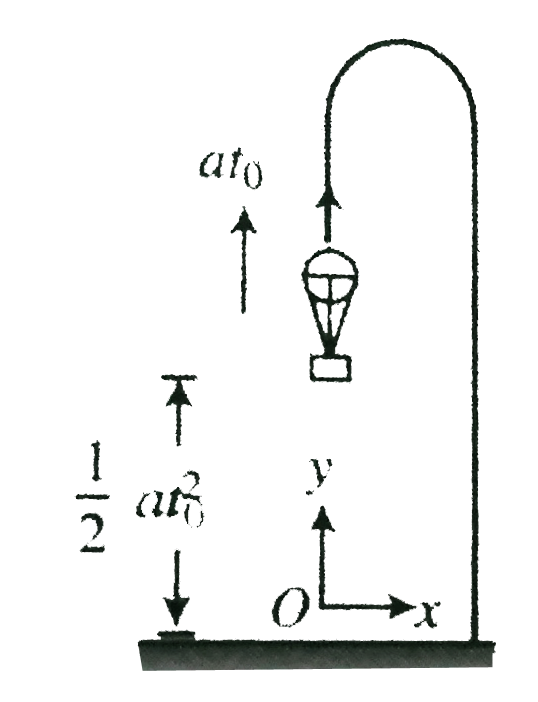 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One

A balloon starts rising with constant acceleration 2m/s2 from ground at t=0s. A stone is dropped at t=5s. S-t graph for the given situation is shown in figure answer the following
t1 isA4 sB6 sC2 sD1 s - Question 2 - Select One
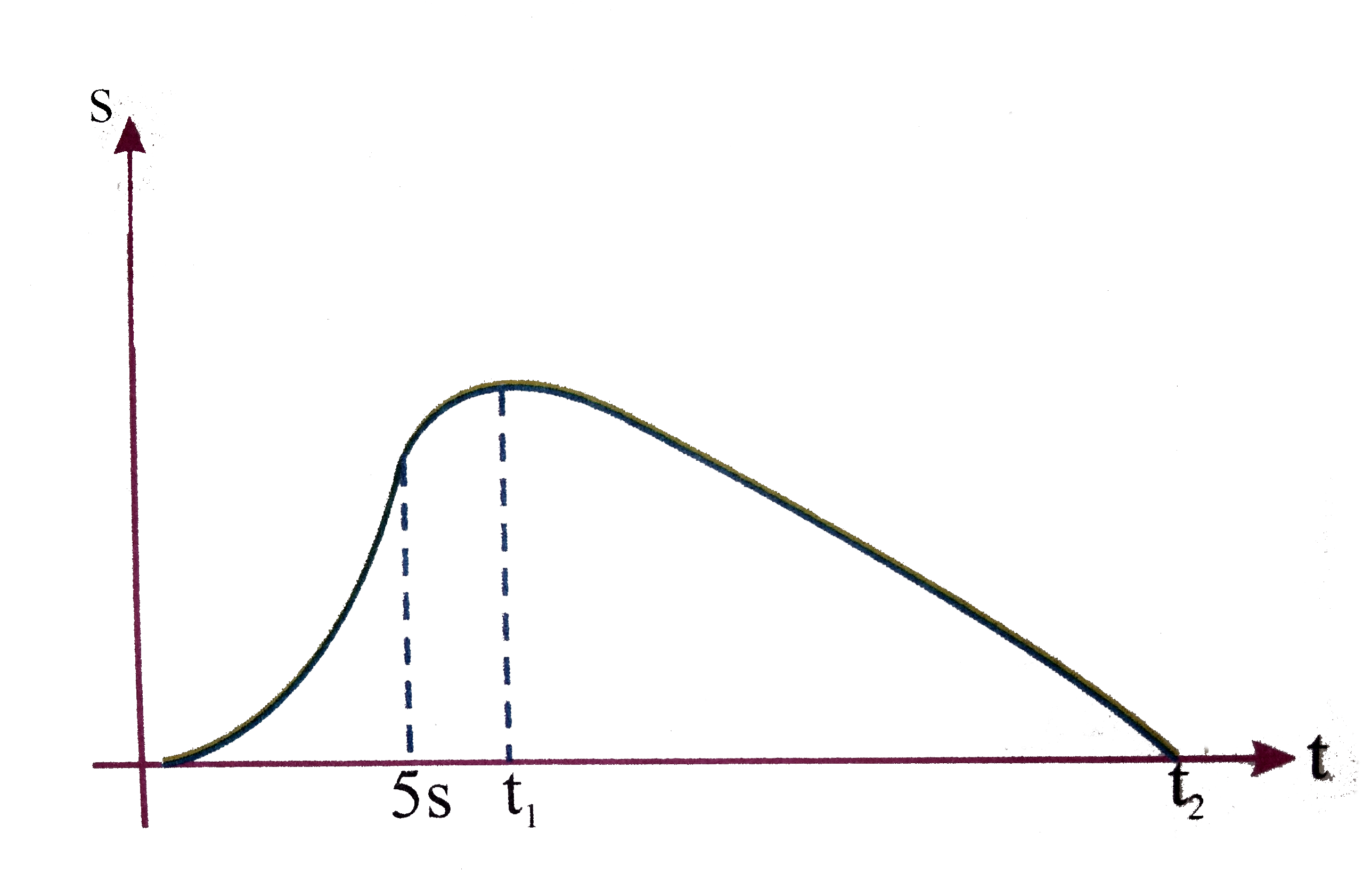
A balloon starts rising with constant acceleration 2m/s2 from ground at t=0s. A stone is dropped at t=5s. S-t graph for the given situation is shown in figure answer the following
t2 isA4 sB4.45 sC3.45 sD9.45 s - Question 3 - Select One
A car starts from rest and moves with constant acceleration. In first t seconds it covers distance x. Then distance covered by it in next t seconds will be:-
AxB2 xC3 xD4 x
A balloon starts from the state of rest from the ground with constant acceleration g/n. after time T, a stone is dropped from the balloon. If stone takes time T to reach the ground then calculate value of n.
View SolutionA disc starts rotating with a constant angular acceleration of 1rad/s2 about a fixed vertical axis perpendicular to its plane and passing through its centre. A coin of mass 10gm is placed on the disc at a distance of 10cm from the axis. The coefficent of friction between the disc and the coin is 0.2. The value of the frictional force on the coin at t=1s will be
View SolutionAn elevator car whose floor to ceiling distance is equal to 2.7m starts ascendiung with constant acceleration 1.2ms2, 2 sec after the start a bolt begins falling from the ceiling of the car. Answer the following question g=9.8m/s2
Distance covered by the bolt during the free fall time w.r.t. ground frame.View Solutiontwo cars start moving from rest with uniform acceleration a=4m/s2 and 8m/s2 towards each other from points A and B. the distance between points is 96 m
View SolutionAn elevator, in which a man is standing, is moving upward with a constant acceleration of 2m/s2. At some instant when speed of elevator is 10m/s, the man drops a coin from a height of 1.5m. Find the time taken by the coin to reach the floor.
View Solution

