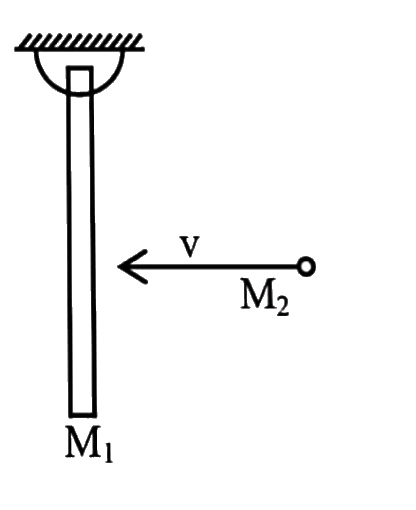
A slender rod is hinged at its top end and hanging freely in a vertical position. A tiny ball, moving horizontally, hits the lower end of the rod elastically and comes to rest. The ratio of the mass of rod to the mass of the ball must be
3:2
3:1
5:3
insufficient data
The correct Answer is:2
mv0l=ml23ω
v0=ωl⇒M=3m
Topper's Solved these Questions
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (A)
32 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART (B)
3 Videos
- TEST PAPERSBOOK - BANSALCHAPTER - TEST PAPERSEXERCISE - PHYSICS PART- C
4 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform rod of mass M1 is hinged at its upper end as shown in the figure . A particle of mass M2 which is moving horizontally, strikes the rod elastically at its midpoint. If the particle comes to rest after collision then the value of M1M2 is
View SolutionA uniform rod of mass m and length l pivoted at one of its top end is hanging freely in vertical plane. Another identical rod moving horizontally with velocity v along a line passing through its lower end hits it and sticks to it. The two rods were perpendicular during the hit and later also they remain perpendicularly connected to each other. Find the maximum angle turned by the two-rod system after collision.
View Solution
Knowledge Check
A uniform rod is resting freely over a smooth horizontal plane. A particle moving horizontally strikes at one end of the rod normally and gets stuck. Then
Athe momentum of the particle is shared between the particle and the rod and remains conserved.Bthe angular momentum about the mid-point of the rod before and after the collision is equal.Cthe angular momentum about the centre of mass of the combination before and after the collision is equal.D. the centre of mass of the rod particle system starts to move translationally with the original momentum of the particle.A uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
A2[√2gl]B√2glC2[√gl]D√glA uniform rod of mass M is hinged at its upper end. A particle of mass m moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision find the value of M/m?
 A3/4B4/3C2/3DNone of these
A3/4B4/3C2/3DNone of these
A rod is hinged vertically at one end and is forced to oscillate in a vertical plane with hinged end at the top, the motion of the rod:
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionConsider a rod of mass M and length L pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass M moving horizontally at a speed v strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.
View SolutionA uniform rod of mass M1 is hinged at its upper end. A particle of mass M2 moving horizontally strikes the rod at its mid point elastically. If the particle comes to rest after collision, the value of M1M2 is -

View SolutionA rod of uniform cross-section of mass M and length L is hinged about an end to swing freely in a vertical plane. However, its density is non uniform and varies linearly from hinged end to the free end doubling its value. The moment of inertia of the rod, about the rotation axis passing through the hinge point
View Solution