Let A,B and I (identity matrix) be the matrices of order 4 such that A=[aij]4×4' where alj{0ifi=j1ifi≠jandA=B−I
Column-IColumn-II(A)|B|=(P)4(B)∣∣B2−4B+I∣∣=(Q)0(C)−4+∣∣B3+B2−8B∣∣=(R)−1(D)−1+∣∣A−1+I∣∣is greater than(S)−4(T)1
The correct Answer is:A-Q ; B-T ; C-S ; D-R , S
To solve the problem, we need to analyze the matrices A, B, and the identity matrix I of order 4. Let's break down the steps to find the required determinants and match the options.
Step 1: Define Matrix A
Matrix A is defined such that:
- aij=0 if i=j (diagonal elements)
- aij=1 if i≠j (off-diagonal elements)
Thus, the matrix A looks like this:
A=⎛⎜
⎜
⎜⎝0111101111011110⎞⎟
⎟
⎟⎠
Step 2: Define Matrix B
Given that A=B−I, we can express B as:
B=A+I
Where I is the identity matrix:
I=⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠
Adding A and I:
B=⎛⎜
⎜
⎜⎝0111101111011110⎞⎟
⎟
⎟⎠+⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠=⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠
Step 3: Calculate |B|
The determinant of matrix B can be calculated. Since all rows are identical, the determinant is:
|B|=0
This matches with option Q.
Step 4: Calculate |B2−4B+I|
First, we calculate B2:
B2=B⋅B=⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠⋅⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠=⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠
Now calculate |B2−4B+I|:
B2−4B+I=⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠−⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠+⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠
This results in:
=⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠=I
Thus, |B2−4B+I|=1.
Step 5: Calculate |−4+|B3+B2−8B||
Next, we calculate B3:
B3=B2⋅B=⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠⋅⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠=⎛⎜
⎜
⎜⎝16161616161616161616161616161616⎞⎟
⎟
⎟⎠
Now calculate B3+B2−8B:
B3+B2−8B=⎛⎜
⎜
⎜⎝16161616161616161616161616161616⎞⎟
⎟
⎟⎠+⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠−⎛⎜
⎜
⎜⎝8888888888888888⎞⎟
⎟
⎟⎠
This results in:
=⎛⎜
⎜
⎜⎝12121212121212121212121212121212⎞⎟
⎟
⎟⎠
Thus, the determinant |B3+B2−8B|=0.
Step 6: Calculate |−1+|A−1+I|>−4
To find A−1, we note that A is singular (its determinant is 0), hence A−1 does not exist. Therefore, |A−1+I| cannot be computed.
Conclusion
From the calculations:
- |B|=0 matches with Q.
- |B2−4B+I|=1 matches with T.
- |B3+B2−8B|=0 matches with S.
- A−1 does not exist, so D cannot be matched.
Matrix A is defined such that:
- aij=0 if i=j (diagonal elements)
- aij=1 if i≠j (off-diagonal elements)
A=⎛⎜
⎜
⎜⎝0111101111011110⎞⎟
⎟
⎟⎠
Given that A=B−I, we can express B as:
B=A+I
Where I is the identity matrix:
I=⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠
B=⎛⎜
⎜
⎜⎝0111101111011110⎞⎟
⎟
⎟⎠+⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠=⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠
The determinant of matrix B can be calculated. Since all rows are identical, the determinant is:
|B|=0
This matches with option Q.
First, we calculate B2:
B2=B⋅B=⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠⋅⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠=⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠
B2−4B+I=⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠−⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠+⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠
This results in:
=⎛⎜
⎜
⎜⎝1000010000100001⎞⎟
⎟
⎟⎠=I
Thus, |B2−4B+I|=1.
Next, we calculate B3:
B3=B2⋅B=⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠⋅⎛⎜
⎜
⎜⎝1111111111111111⎞⎟
⎟
⎟⎠=⎛⎜
⎜
⎜⎝16161616161616161616161616161616⎞⎟
⎟
⎟⎠
B3+B2−8B=⎛⎜
⎜
⎜⎝16161616161616161616161616161616⎞⎟
⎟
⎟⎠+⎛⎜
⎜
⎜⎝4444444444444444⎞⎟
⎟
⎟⎠−⎛⎜
⎜
⎜⎝8888888888888888⎞⎟
⎟
⎟⎠
This results in:
=⎛⎜
⎜
⎜⎝12121212121212121212121212121212⎞⎟
⎟
⎟⎠
Thus, the determinant |B3+B2−8B|=0.
To find A−1, we note that A is singular (its determinant is 0), hence A−1 does not exist. Therefore, |A−1+I| cannot be computed.
From the calculations:
- |B|=0 matches with Q.
- |B2−4B+I|=1 matches with T.
- |B3+B2−8B|=0 matches with S.
- A−1 does not exist, so D cannot be matched.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If A=[aij] is a square matrix of order 2 such that aij={1when i≠j0when i=j that A2 is :
A[1010]B[1100]C[1110]D[1001]If matrix A=[aij]4×4 such that
aij={3i=j0i≠j and det (adj (adj A)) = 3k , then k isA12B20C28D36If matrix A=[aij]3×3, matrix B=[bij]3×3, where aij+aji=0 and bij−bji=0∀i, j, then A4⋅B3 is
ASingularBZero matrixCSymmetricDSkew-Symmetric matrix
Let A&B are two non singular matrices of order 3 such that A+B=I & A−1+B−1=2I then |adj(4AB)| ,is (where adj(A) is adjoint of matrix A)
View SolutionIf matrix A=([aij])2×2 , where aij={1, if i≠j0, if i=j , then A2 is equal to I (b) A (c) O (d) I
View SolutionMatch Column - I with Column - II
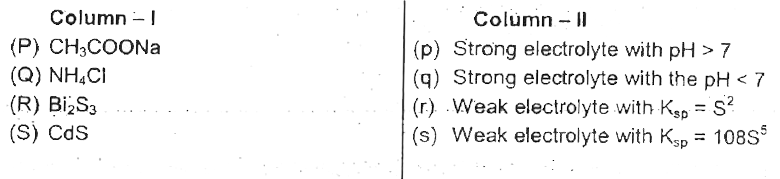
PQRS(A)1243(B)2143(C)4132(D)4321
View SolutionIf aj=0(i≠j)andaij=4(i=j),,then the matrix A=[aij]n×n is a matrix
View SolutionLet A and B are square matrices of order 3. If |A|=4,|B|=6,B=A−2Iand∣∣adj(I−2A−1)∣∣=k, then the value of k is equal to
View Solution
