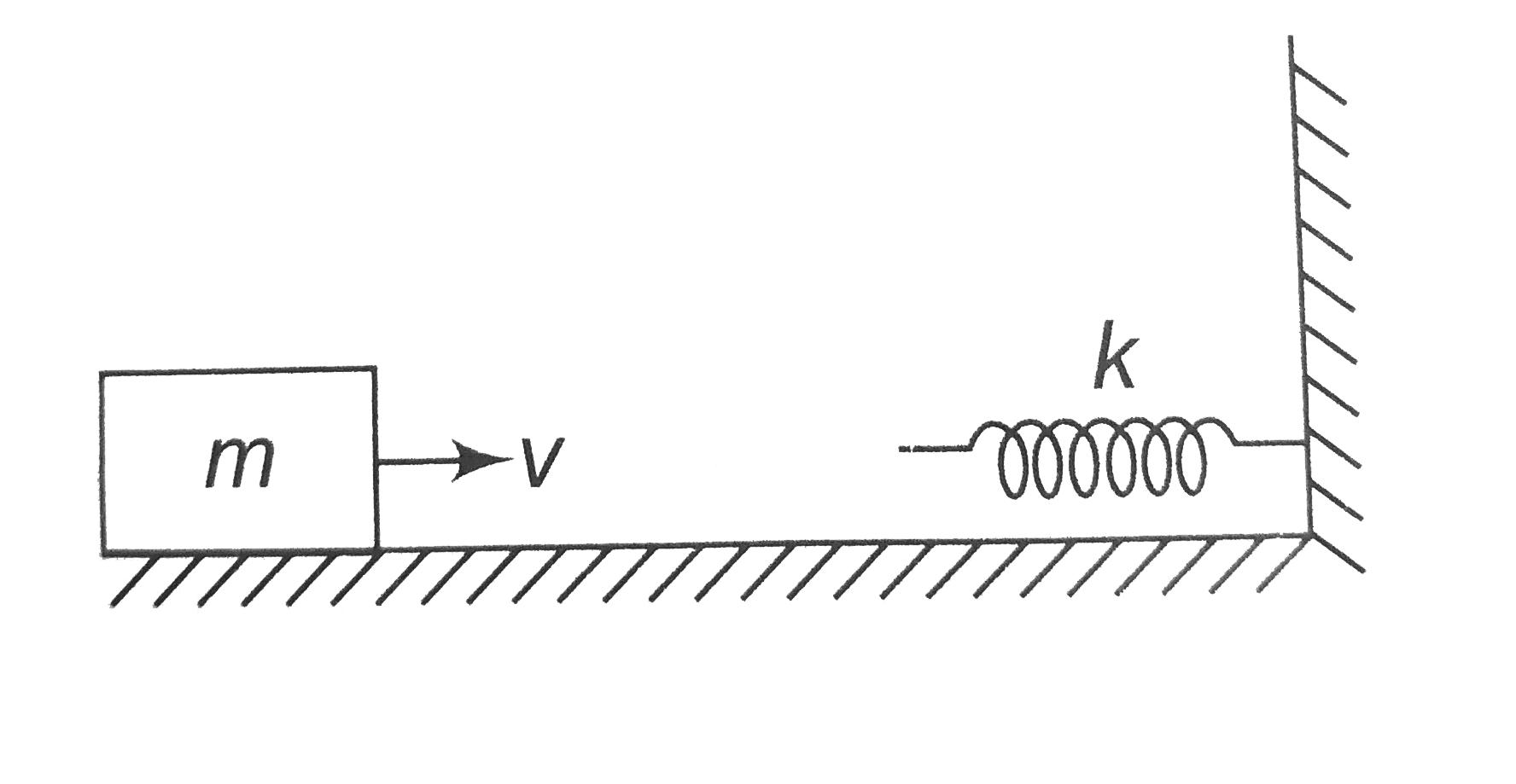
A block of mass m lies on a horizontal frictionless surface and is attached to one end of a horizontal spring (with spring constant k) whose other end is fixed . The block is intinally at rest at the position where the spring is unstretched (x=0). When a constant horizontal force →F in the positive direction of the x−axis is applied to it, a plot of the resulting kinetic energy of the block versus its position x is shown in figure. What is the magnitude of →F ?
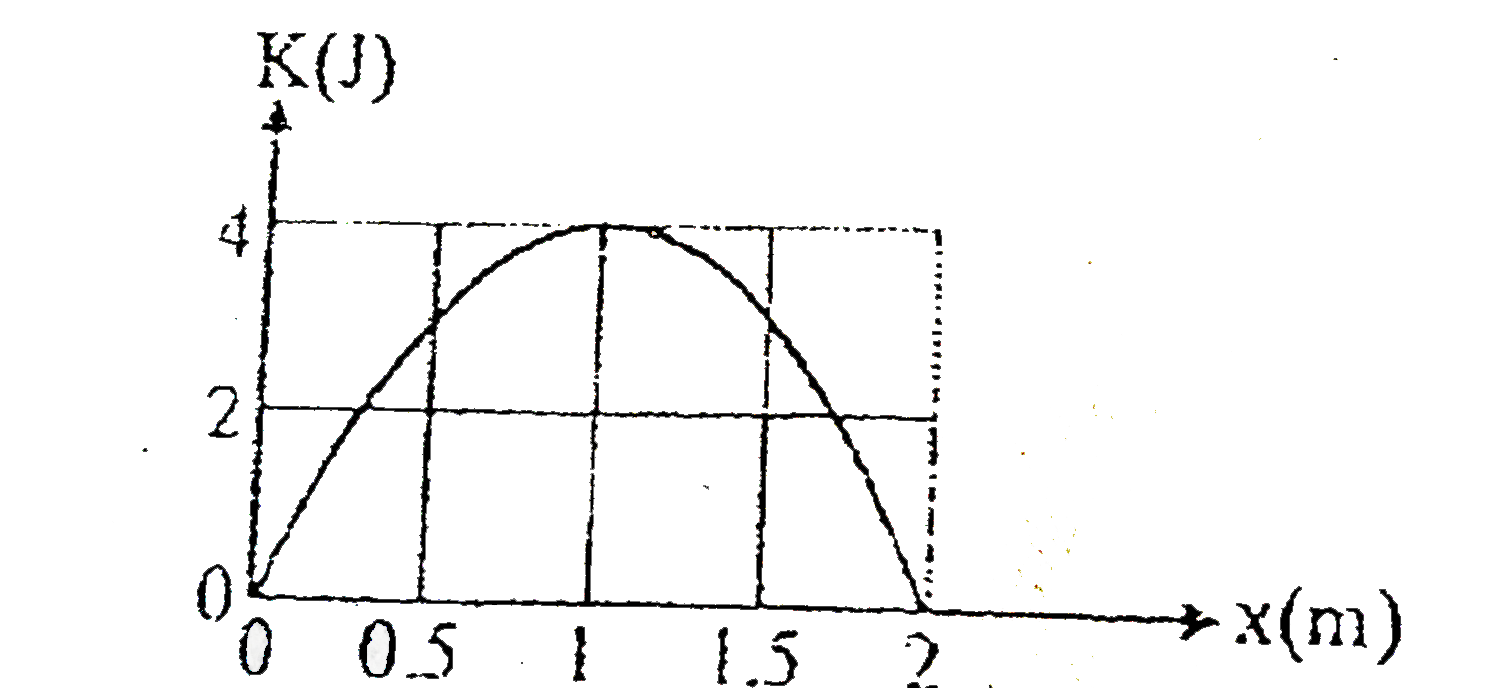
2N
4N
8N
16N
The correct Answer is:C
At equilibrium (Net Force =0 and velocity is maximum), F=kx & Fx−12kx2=ΔK.E=4 here x=1m
Topper's Solved these Questions
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLENCHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLENCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLENCHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
A block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View SolutionA block of mass m, lying on a smooth horizontal surface, is attached to a spring (of negligible mass) of spring constant k. The other end of the spring is fixed, as shown in the figure. The block is initally at rest in its equilibrium position. If now the block is pulled withe a constant force F, the maximum speed of the block is :

View Solution
Knowledge Check
A block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
Av√m/2kBv√m/kCv√m/4kDmv2/4kA block of mass 4kg slides on a horizontal frictionless surface with a speed of 2m/s. It is brought to rest in compressing a spring in its path. If the force constant of the spring is 400N/m, by how much the spring will be compressed
A2×10−2mB0.2mC20mD200mA 1.5−kg block is initially at rest on a horizontal frictionless surface when a horizontal force in the positive direction of x-axis is applied to the block. The force is given by →F=(4−x2)→iN, where x is in meter and the initial position of the block is x=0.
The maximum positive displacement x isA(a) 2√3B(b) 2mC(c) 4mD(d) √2m
A block of mass M is kept on a rough horizontal surface and is attached with massless spring of force constant k .The minimum constant force applied on the other end of the spring to lift the block is
View SolutionA large fake cookie sliding on a horizontal surface is attached to one end of a horizontal spring with spring constant k=360 N/m, the other end of the spring is fixed in place. The cookie has a kinetic energy of 20.0 J as it passes through the spring's equilibrium position. As the cookie slides, a frictional force of magnitude 10.0 N acts on it . (a) How far will the cookie slide from the equilibrium position before coming momentarily to rest ? (c) What will be the kinetic energy of the cookie as it slides back through the equilibrium position ?
View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
View SolutionAn ideal spring with spring constant k is hung from the ceiling and a block of mass M is attached to its lower end. The mass is released with the spring initially unstretched. Then the maximum extension in the spring is
View SolutionA 1.5kg block is initially at rest on a horizontal frictionless surface. A horizontal force →F=(4−x2)ˆi is applied on the block. Initial position of the block is at x=0. The maximum kinetic enery of the block between x=0 and x=2m is
View Solution
