A chain of length L and mass m is placed upon a smooth surface. The le

A uniform chain of length $l$ and mass m is placed on a smooth table with one-fourth of its length hanging over the edge. The work that has to be done to pull the whole chain back onto the table is :
A $\frac{1}{4} m g l$
B $\frac{1}{8} m g l$
C $\frac{1}{16} m g l$
D $\frac{1}{32} m g l$
A chain of length L and mass per unit length $ρ$ is piled on a horizontal surface. One end of the chain is lifted vertically with constant velocity by a force P.
AP as function of height x of the end above the surface will be $ρ (g x + v^{2})$
Bno energy will loss in this process.
Cwork done by force will be $\frac{1}{2} ρ g L^{2} + ρ v^{2} L$
Dloss in energy $\frac{1}{2} ρ g L v^{2}$
A chain of length L is placed on a horizontal surface as shown in figure. At any instant x is the length of chain on rough surface and the remaining portion lies on smooth surface. Initially $x = 0$ . A horizontal force p is applied to the chain (as shown in figure) in the duration from $x = 0 \to x = L$ . For chain to move with constant speed
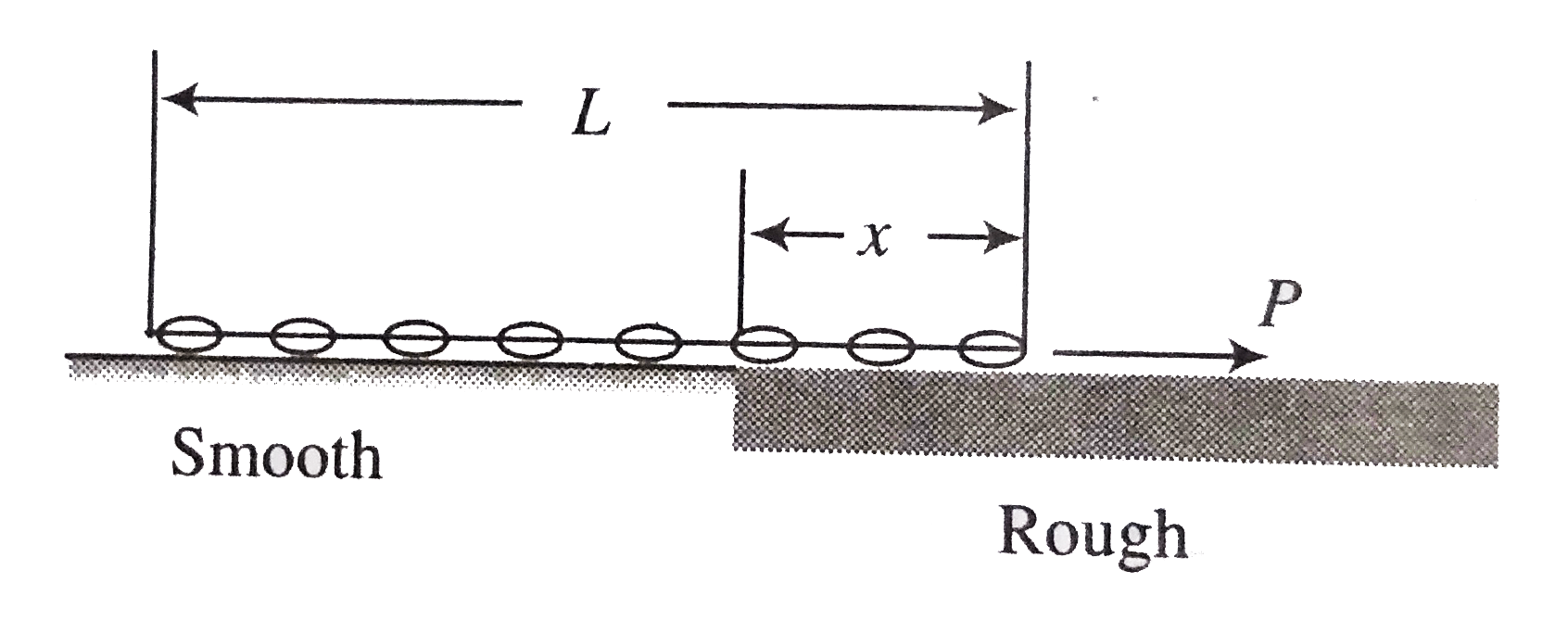AThe magnitude of P should increases with time
BThe magnitude of P should decreases with time
CThe magnitude of P should increases first and then decrease with time
DThe magnitude of P should decrease first and then increases with time

A chain of length $L$ and mass $m$ is placed upon a smooth surface. The length of $B A$ is $(L - b)$ . Calculate the velocity of the chain when its and reaches $B$