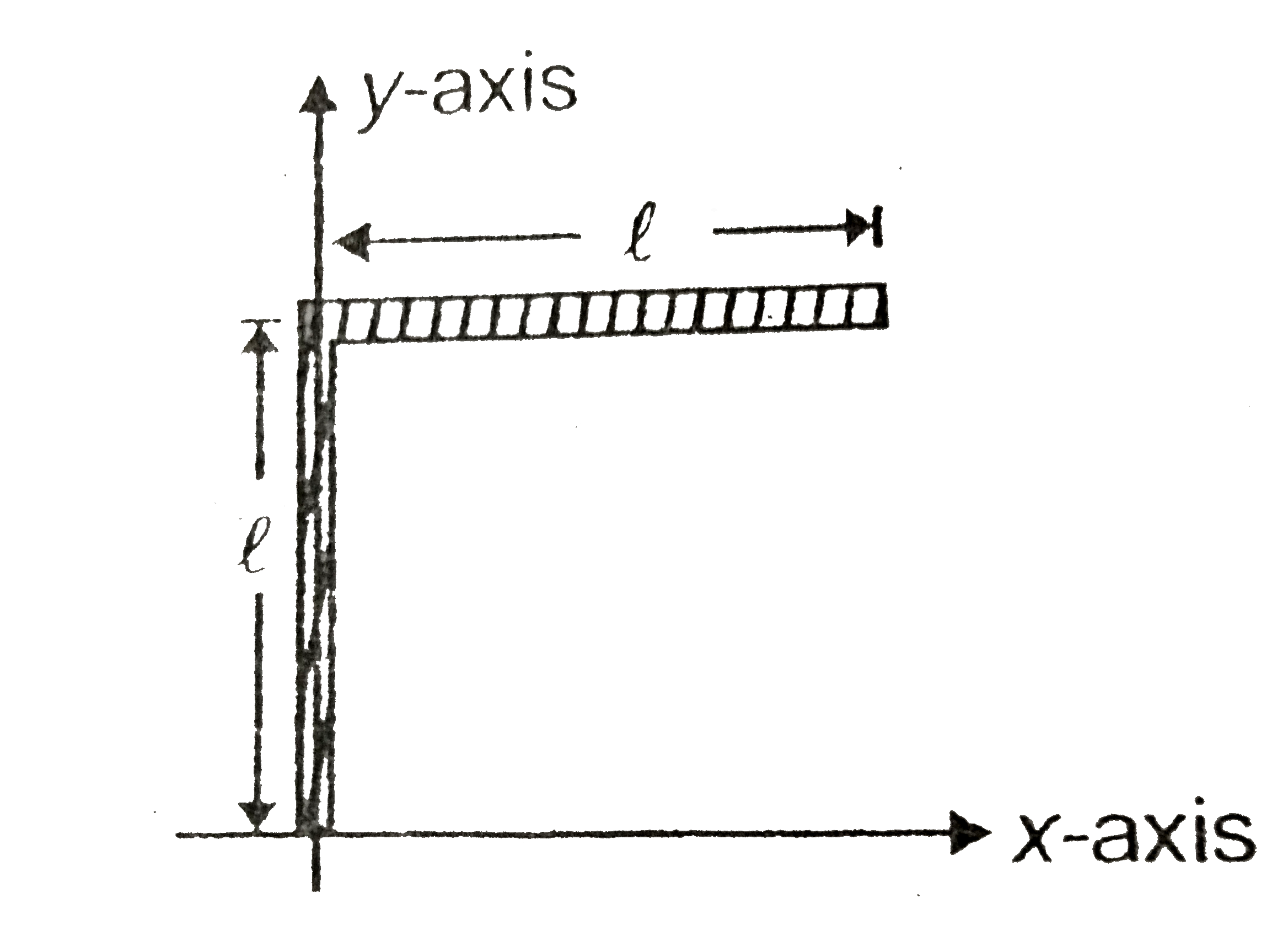Infinite rods of uniform mass density and length L,L/2,L/4….. Are placed one upon another upto infinite as shown in figure. Find the x-coordinate of centre of mass.

0
L/3
L/2
2L/3
The correct Answer is:A
Step by step video, text & image solution for Infinite rods of uniform mass density and length L,L/2,L/4….. Are placed one upon another upto infinite as shown in figure. Find the x-coordinate of centre of mass. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Two identical thin uniform rods of length L each are joined to form T shape as shown in the figure. The distance of centre of mass from D is
 A0BL/4C3L/4DL
A0BL/4C3L/4DL - Question 2 - Select One
A thin uniform rod of length L is bent at its mid point as shown in the figure. The distance of the centre of mass from the point O is
 AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2)
AL2sin(θ2)BL2cos(θ2)CL4sin(θ2)DL4cos(θ2) - Question 3 - Select One
Four identical rods of mass M and length L are placed on one another on the table so as to produce the maximum overhang as shown in figure. The maximum total overhang will be :
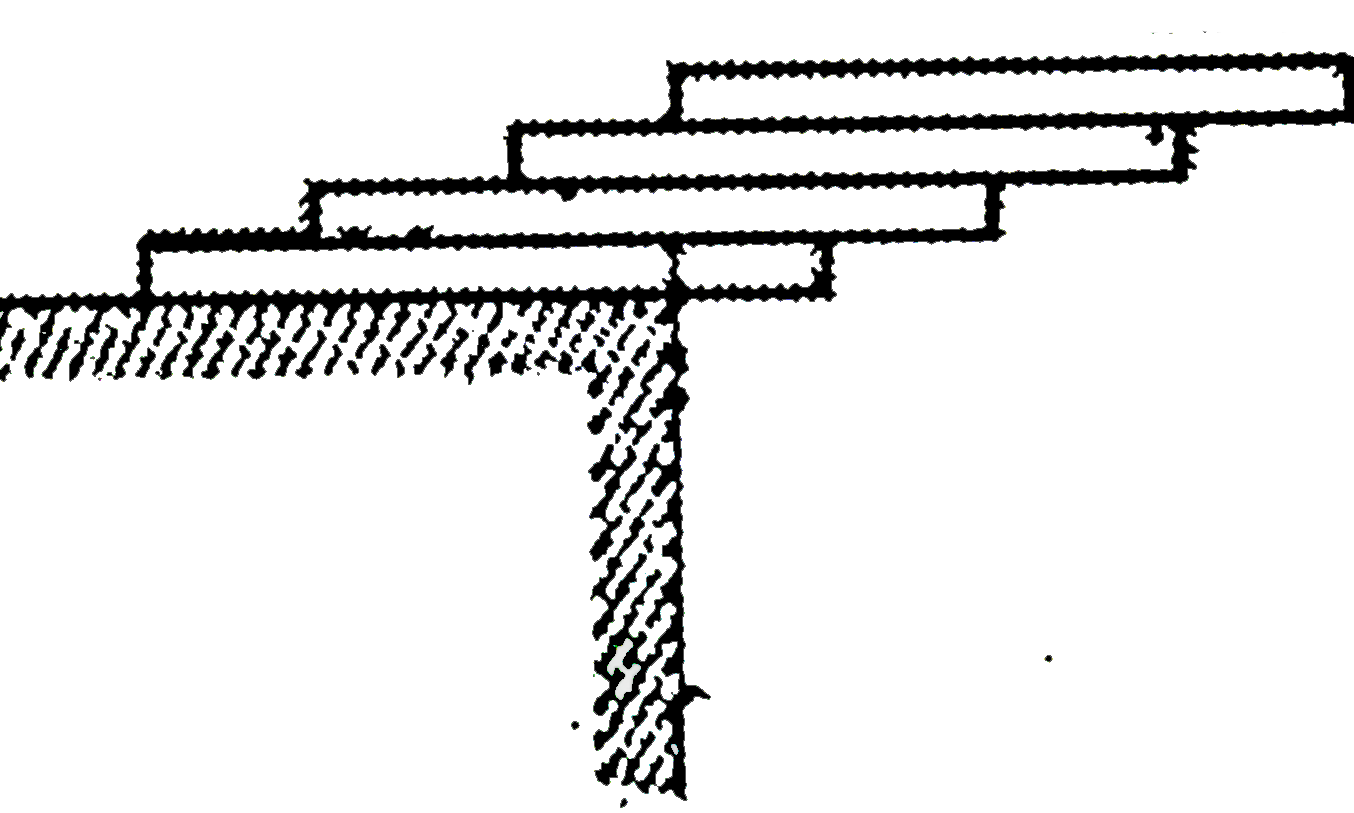 A3L4B24L25C25L24D4L3
A3L4B24L25C25L24D4L3
Six rods of the same mass m and length ? are arranged as shown in figure. Calculate the coordinate of the centre of mass of the system:- У >X
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass (a) variea with x as:
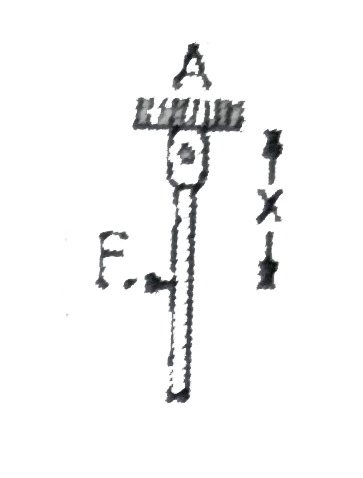 View Solution
View SolutionA rod of mass m and length l is hinged at one of its end A as shown in figure. A force F is applied at a distance x from A. The acceleration of centre of mass a varies with x as
 View Solution
View SolutionA rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?
 View Solution
View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
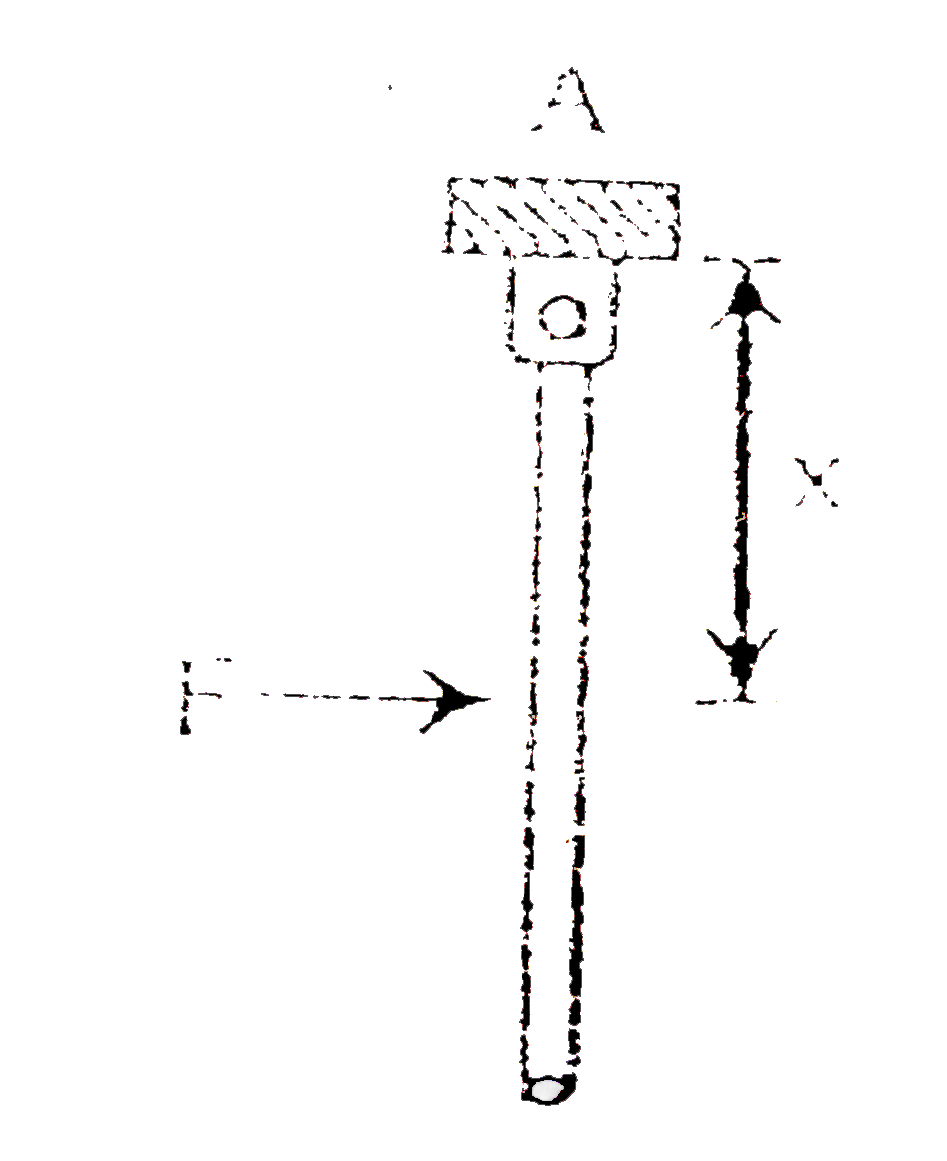 View Solution
View Solution