A rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass? 
23L
14L
13L
12L
The correct Answer is:A
Xcm=1M∫xdm=1M∫L0x(2mL2x)dx=2L3
Similar Questions
The linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionFind coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View Solution
Knowledge Check
- Question 1 - Select One
Find centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
A3l4(3a+b2a+b)B3l4(2a+b3a+b)Cl4(2a+b3a+b)Dl(2a+b3a+b) - Question 2 - Select One
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
AL/2B2L/3CL/4DL/5 - Question 3 - Select One
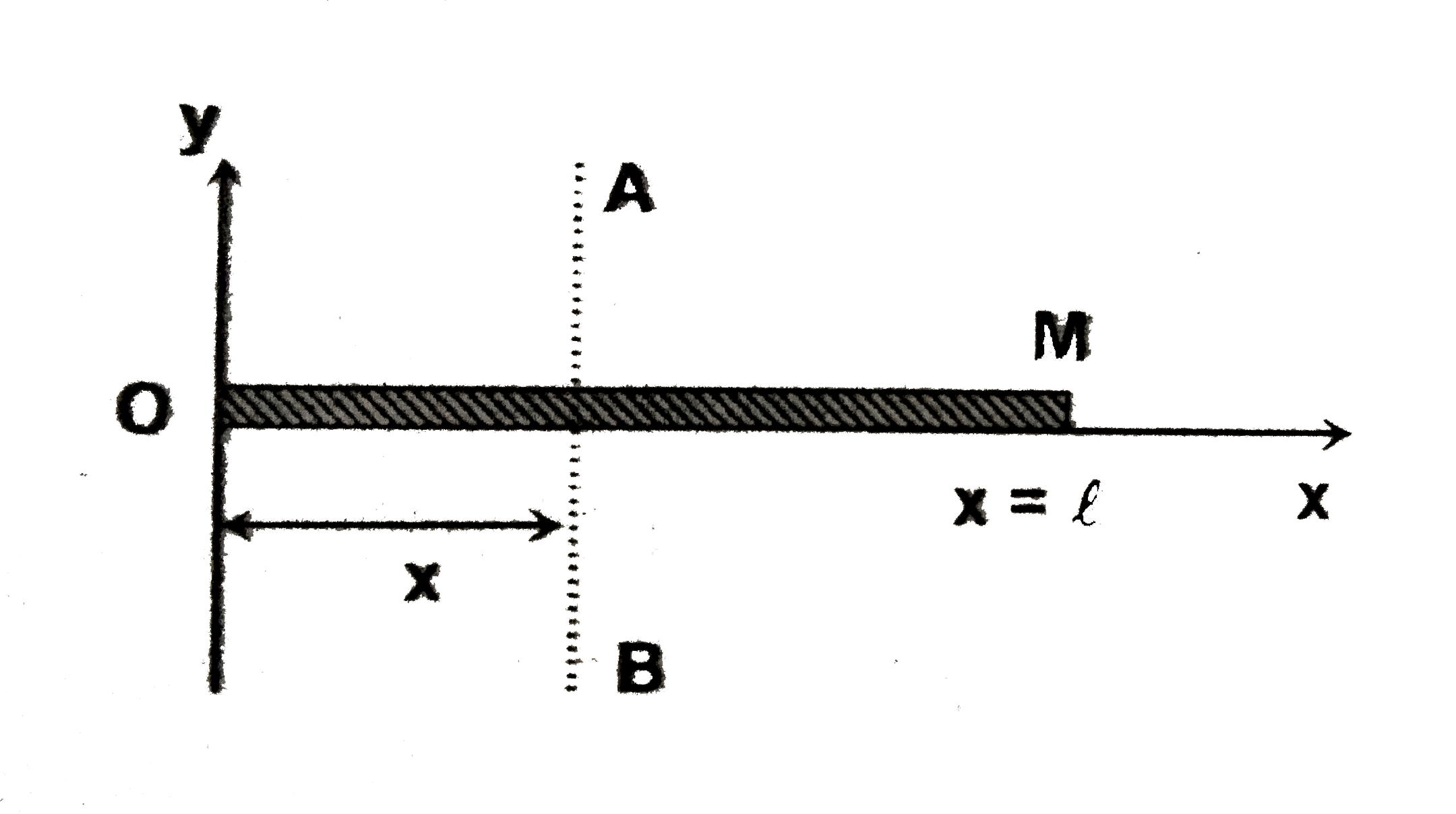
A non uniform rod OM (of length l m) is kept along x-axis and rotating about an axis AB, which is perpendicular to rod as shown in the figure. The rod has linear mass densty that varies with the distance x from left end of the rod according to λ=λ0(x3L3)
Where unit of λ0 is kg/m. What is the value of x so that moment of inertia of rod about axis AB (IAB) is minimum?A7l15B2l5C8l15D4l5
A rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) λ of the rod varies with the distance x from the origin as λ=Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
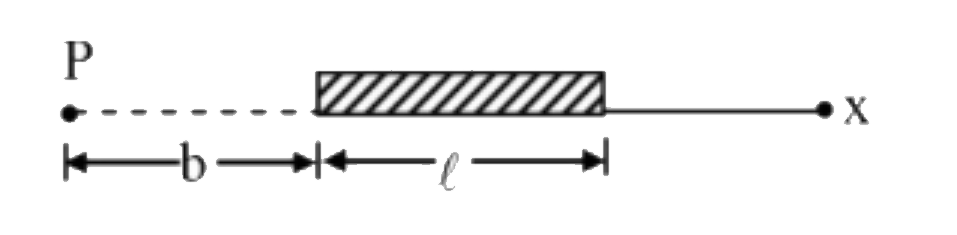
View SolutionA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
 View Solution
View SolutionA rod of lengthL and mass M0 is bent to form a semicircular ring as shown. The M.I. about X'X is
 View Solution
View Solution
