A particle moves along the X-axis as x=u(t−2s)=at(t−2)2.
The initial velocity of the particle is u
The acceleration of the particle is a
The acceleration of the particle is 2a
At t=2s particle is at the origin
The correct Answer is:C, D
x=u(t−2)+a(t−2)2…(i)
v=dxdt=u+2a(t−2)
Therefore v(0)=u−4a
a=d2xdt2=2a Hence [C]
x(2)=0[From (i)]. Hence [D]
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-036videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Assertion-Reason20videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-0155videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
A particle is moving along the x-axis such that s=6t−t2, where s in meters and t is in second. Find the displacement and distance traveled by the particle during time interval t=0 to t=5s.
View SolutionA particle moves along the x-axis so that its position is given x=2t3–3t2 at a time t second. What is the time interval duringwhich particle will be on the negative half of the axis?
View Solution
Knowledge Check
- Question 1 - Select One
A particle moves along x-axis as x=t(t−2)+(t−2)2 . Which of the following is true?
AThe initial velocity of particle is 4BThe accekeration of particle varies with timeCThe particle is at origin at t = 0DNone of these - Question 2 - Select One
A particle moves along x-axis as x=4(t−2)+a(t−2)2
Which of the following is true?AThe initial velocity of particle is 4Bthe acceleration of particle is 2aCThe particle is at origin at t=0Dnone of these - Question 3 - Select One
A particle moves along the x-axis in such a way that its x-co-ordinate varies with time as x=2–5t+6t2.
The initial velocity and acceleration of particle will respectively be-A–5 m/s, 12 m/sB5 m/s, –12 m/sC–5 m/s, –12 m/sD5 m/s, 12 m/s
The displacement -time equation of a particle moving along x -axis is x=t33−t22+20The acceleration -velocity equation of the particle is a2=KV+1 Then the value of K is
View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=1sto t=3s.View SolutionA particle moves along the X-axis. Its X-coordinate varies with time according to the expression x=4t+2r2, where x is in meters and t is in seconds. The position-time graph for this motion is shown in the figures previously. Note that the particle moves in the negative X-direction for the first second of motion, is at rest at the moment t=1s, and then heads back in the positive X-direction for t>1s.
Find the displacement of the particle in the time interval t=0 s to t=1 s.View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
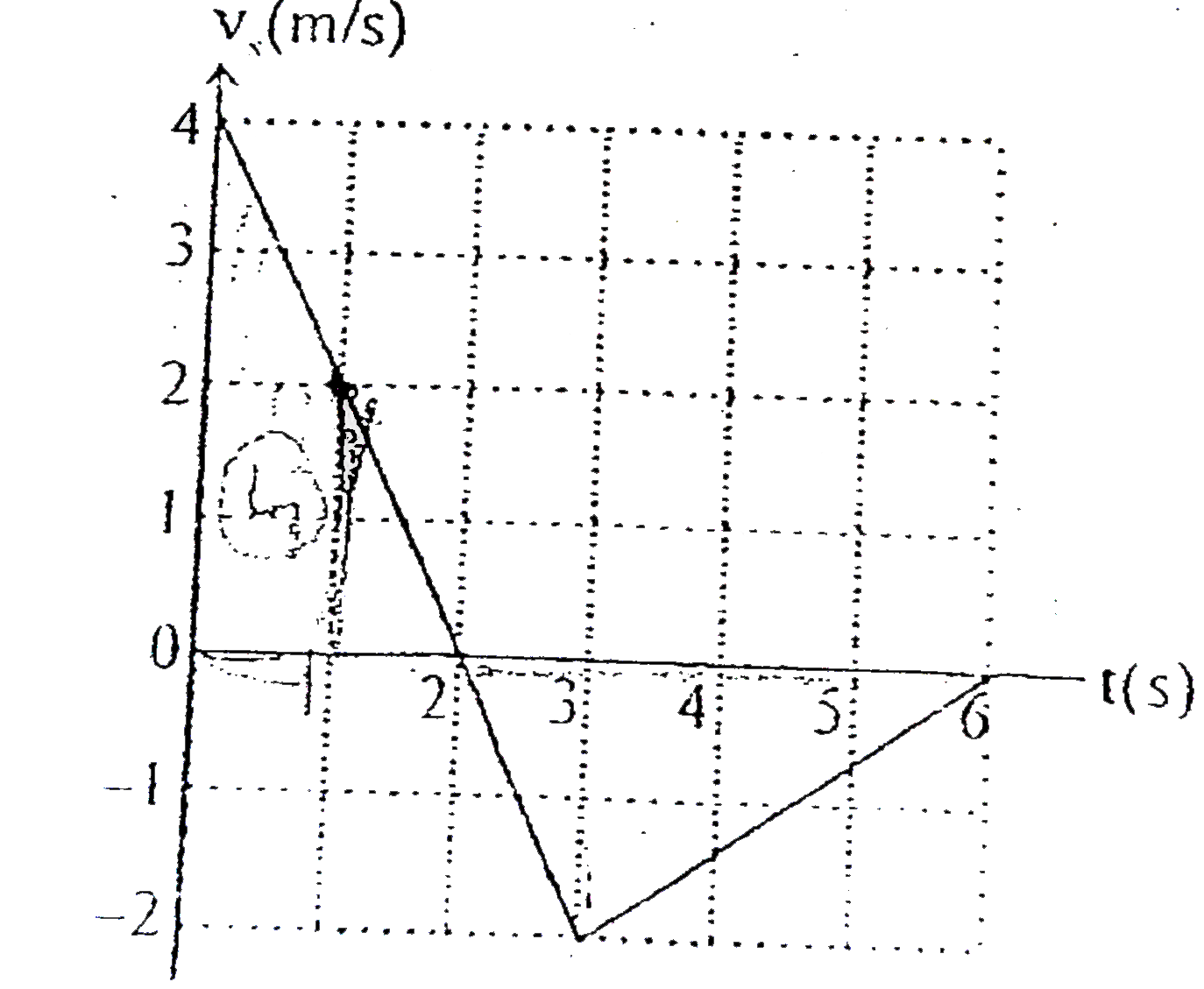 View Solution
View SolutionA particle moves along the X-axis. The position x of particle w.r.t. time from origin given by x=b0+b1+b2t2 .The acceleration of particle is
View Solution

