A ring rotates about z axis as shown in figure. The plane of rotation is xy. At a certain instant the acceleration of a particle P (shown in figure) on the ring is . Find the angular acceleration of the ring & the abgular velocity at that instant. Radius of the ring is 2m.

The correct Answer is:
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Exercise-04[B]14videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Exercise-05 [A]11videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#73videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
A smooth ring of mass m and radius R=1m is pulled at P with a constant acceleration a=4ms−2 on a horizontal surface such that the plane of the ring lies on the surface. Find the angular acceleration of the ring at the given position. (in rad/s2)
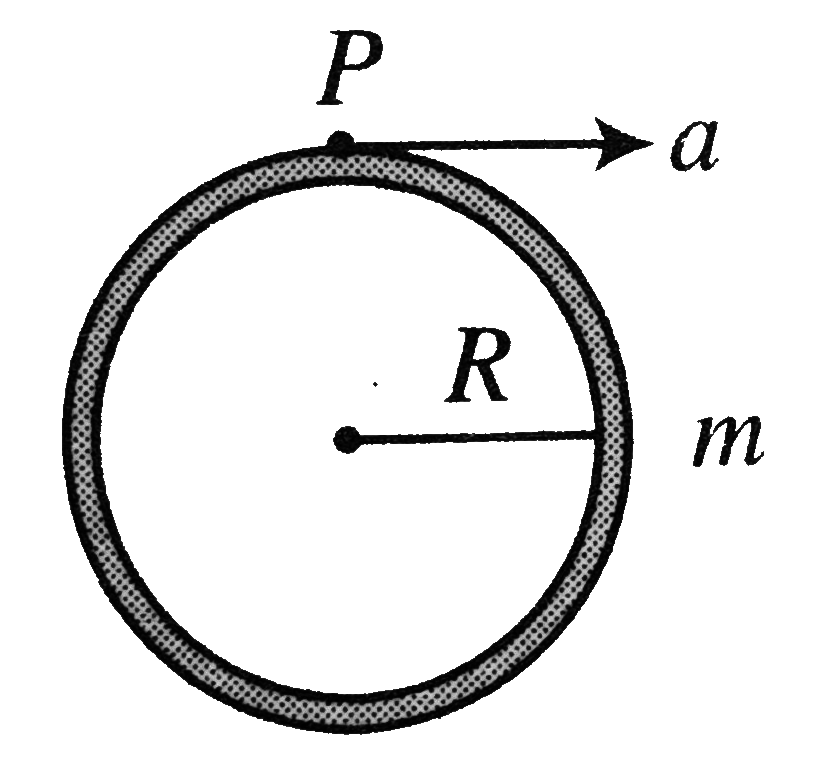 View Solution
View SolutionA particle is rotating about a fixed axis with angular acceleration →α =(3ˆi+ˆj+ˆk) rads2. The tangential acceleration of a point having radius vector (2ˆi−ˆj−ˆk) m from axis of rotation is (in ms2)
View Solution
Knowledge Check
- Question 1 - Select One
A ring of radius R is rotating about axis of ring such that angular velocity is given as = 5t. Find acceleration of a point P on rim after 5 sec
A5RB25RC√650RDNone of these - Question 2 - Select One

A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If ω is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound isAzeroBω2RCaD√a2+(ω2R)2 - Question 3 - Select One
Velocity of a particle at some instant is v=(3ˆi+4ˆj+5ˆk)m/s. Find speed of the particle at this instant.
A12B7C-12D5√2
The velocity and acceleration vectors of a particle undergoing circular motion are v=2ˆim/sanda=2ˆi+4ˆjm/s2 respectively at some instant of time. The radius of the circle is
View SolutionAt a particular instant velocity and acceleration of a particle are (−ˆi+ˆj+2ˆk)m/s and (3ˆi−ˆj+ˆk)m/s2 respectively at the given instant particle's speed is :
View SolutionA constant force F is applied at the top of a ring as shown in figure. Mass of the ring is M and radius is R. Angular momentum of particle about point of contact at time t
 View Solution
View SolutionA particle is moving in a circular path. The acceleration and momentum of the particle at a certain moment are a=(4ˆi+3ˆj)m/s2andp=(8ˆi−6ˆj)kg-m/s. The motion of the particle is
View SolutionA particle is moving in x-y plane. At an instant, it has velocity (4ˆi+4ˆj)m/s and acceleration (3ˆi+5ˆj)m/s2 At that instant, the radius of curvature of its path will be :
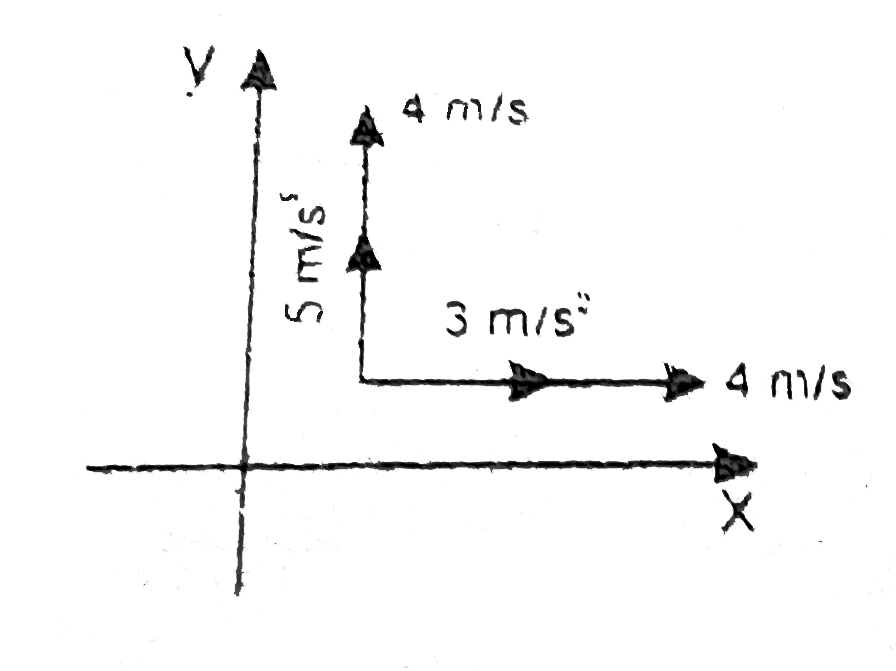 View Solution
View Solution

