Add (i) 710+215 (ii) 2(23)+3(12)
Let's solve the two problems step by step.
Problem (i): Add 710+215
Step 1: Find the LCM of the denominators.
- The denominators are 10 and 15.
- The multiples of 10 are: 10, 20, 30, 40, ...
- The multiples of 15 are: 15, 30, 45, ...
- The least common multiple (LCM) of 10 and 15 is 30.
Step 2: Convert the fractions to have the same denominator.
- For 710:
- Multiply both the numerator and the denominator by 3 (since 10×3=30).
- 7×310×3=2130.
- For 215:
- Multiply both the numerator and the denominator by 2 (since 15×2=30).
- 2×215×2=430.
Step 3: Add the fractions.
- Now we have 2130+430.
- Since the denominators are the same, we can add the numerators:
- 21+430=2530.
Step 4: Simplify the fraction.
- Both 25 and 30 can be divided by 5.
- 25÷530÷5=56.
Final Answer for (i): 56
---
Problem (ii): Add 223+312
Step 1: Convert mixed numbers to improper fractions.
- For 223:
- Multiply the whole number (2) by the denominator (3) and add the numerator (2).
- 2×3+2=6+2=8.
- So, 223=83.
- For 312:
- Multiply the whole number (3) by the denominator (2) and add the numerator (1).
- 3×2+1=6+1=7.
- So, 312=72.
Step 2: Find the LCM of the denominators.
- The denominators are 3 and 2.
- The LCM of 3 and 2 is 6.
Step 3: Convert the fractions to have the same denominator.
- For 83:
- Multiply both the numerator and the denominator by 2 (since 3×2=6).
- 8×23×2=166.
- For 72:
- Multiply both the numerator and the denominator by 3 (since 2×3=6).
- 7×32×3=216.
Step 4: Add the fractions.
- Now we have 166+216.
- Since the denominators are the same, we can add the numerators:
- 16+216=376.
Final Answer for (ii): 376 or 616 if converted back to a mixed number.
---
- The denominators are 10 and 15.
- The multiples of 10 are: 10, 20, 30, 40, ...
- The multiples of 15 are: 15, 30, 45, ...
- The least common multiple (LCM) of 10 and 15 is 30.
- For 710:
- Multiply both the numerator and the denominator by 3 (since 10×3=30).
- 7×310×3=2130.
- For 215:
- Multiply both the numerator and the denominator by 2 (since 15×2=30).
- 2×215×2=430.
- Now we have 2130+430.
- Since the denominators are the same, we can add the numerators:
- 21+430=2530.
- Both 25 and 30 can be divided by 5.
- 25÷530÷5=56.
- For 223:
- Multiply the whole number (2) by the denominator (3) and add the numerator (2).
- 2×3+2=6+2=8.
- So, 223=83.
- Multiply the whole number (3) by the denominator (2) and add the numerator (1).
- 3×2+1=6+1=7.
- So, 312=72.
- The denominators are 3 and 2.
- The LCM of 3 and 2 is 6.
- For 83:
- Multiply both the numerator and the denominator by 2 (since 3×2=6).
- 8×23×2=166.
- Multiply both the numerator and the denominator by 3 (since 2×3=6).
- 7×32×3=216.
- Now we have 166+216.
- Since the denominators are the same, we can add the numerators:
- 16+216=376.
Similar Questions
Knowledge Check
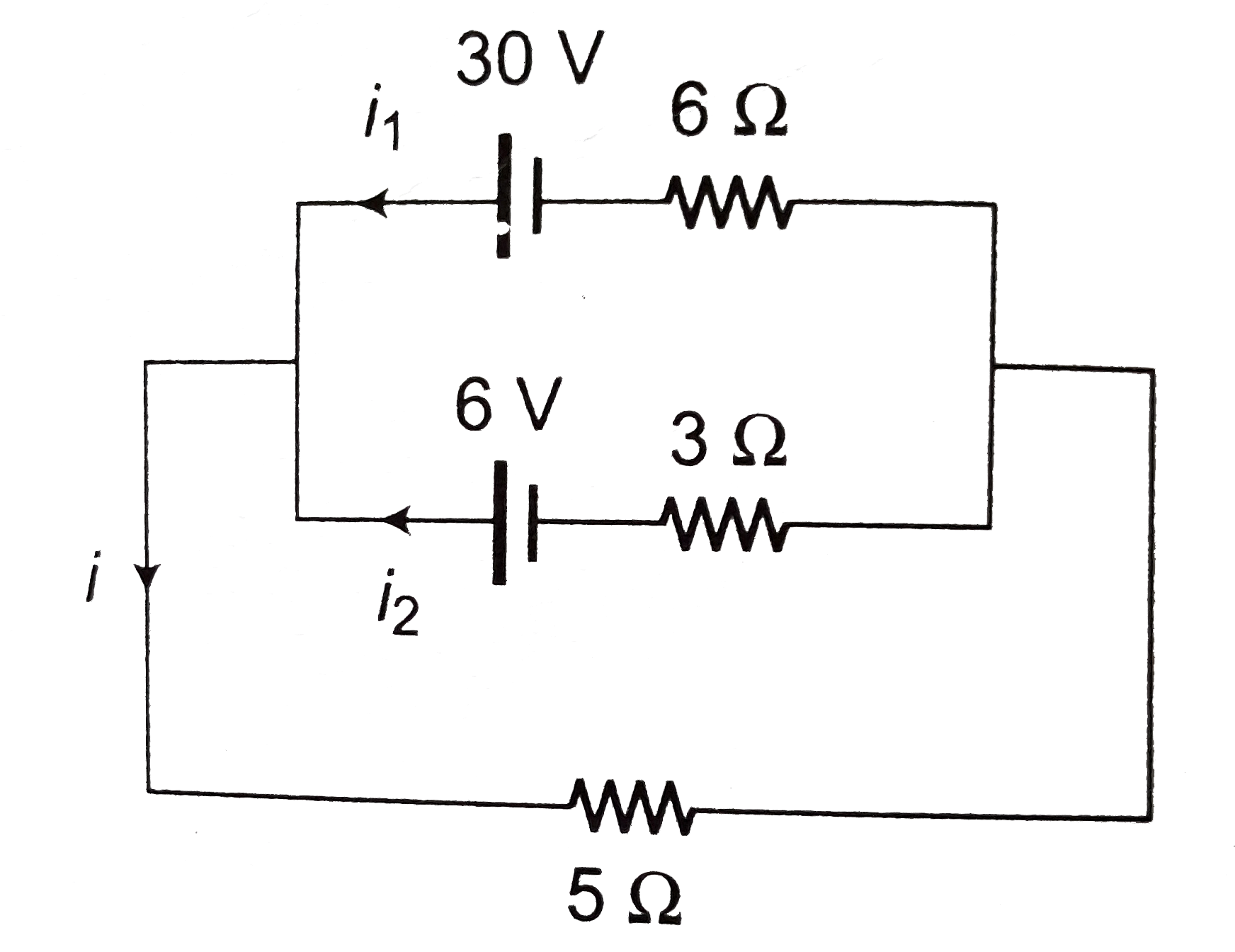 .
.
(i) i=2A
(ii) i1=103A
(iii) i2=−43A.A(i),(ii)B(ii),(iii)C(i),(iii)Dall
Determine:
(i) 23 of 15 pens
(ii) 23 OF 27 balls
(iii) 23 of 36 balloons
View SolutionArrange the following fractions in descending order
(i)34,78,712,1724
(ii)23,35,710,815
View SolutionAdd: (3x2−15x+73)+(−14x2+13x−16)+(−2x2−12x+5)
View SolutionFind the following sums :
(i)1+2+3+…+30
(ii) 12+22+32+…+352
(ii)13+23+33+…+203 .
View SolutionFind the difference:
(i)57−27
(ii)56−34
(iii)315−710
(iv)7−423
(v)3310−1715
(vi)259−1715
View SolutionUse the number line and add the following integers :
(i)9+(−6) (ii)(−3)+7 (iii)8+(−8)
(iv) (−1)+(−3) (v)(−4)+(−7) (vi)(−2)+(−8)
(vii)3+(−2)+(−4) (viii)(−1)+(−2)+(−3) (ix)5+(−2)+(−6)
View SolutionSimplify : (i) 223.215 (ii) (133)7 (iii) 11121114 (iv) 712.812
View Solution
