A horizontal cylindrical tank is half full of water ( refractive index =43) . The space above the water is filled with a light liquid of unknown refractive index (μ). A small laser source (s) can move along the curved bottom of the cylinder and aims a light beam towards the centre of the cylinder. The time needed by the laser beam to travel from the source to the rim of the cylinder depends on position (θ) of the source as shown in the graph. Find μ, it is given that sinθ0=56.
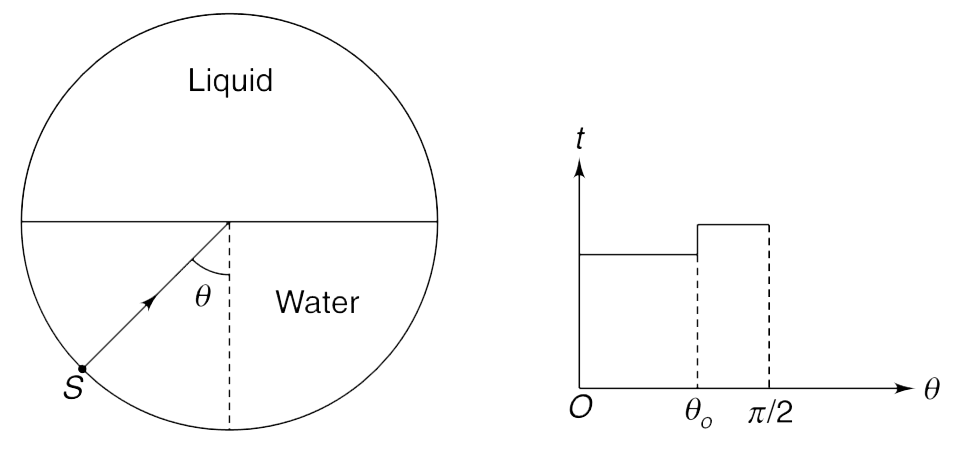
The correct Answer is:μ=109
Step by step video, text & image solution for A horizontal cylindrical tank is half full of water ( refractive index =(4)/(3)) . The space above the water is filled with a light liquid of unknown refractive index (mu). A small laser source (s) can move along the curved bottom of the cylinder and aims a light beam towards the centre of the cylinder. The time needed by the laser beam to travel from the source to the rim of the cylinder depends on position (theta) of the source as shown in the graph. Find mu, it is given that sin theta_(0) = (5)/(6). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 2
62 Videos
- GEOMETRICAL OPTICSBOOK - ARIHANTCHAPTER - GEOMETRICAL OPTICSEXERCISE - Level 3
9 Videos
- ELECTROSTATICSBOOK - ARIHANTCHAPTER - ELECTROSTATICSEXERCISE - Level 3
59 Videos
- MAGNETIC EFFECT OF CURRENTBOOK - ARIHANTCHAPTER - MAGNETIC EFFECT OF CURRENTEXERCISE - Magnetic effect of Current
45 Videos
Similar Questions
(i) Define refractive index of a medium.
(ii) In the following ray diagram, calculate the speed of light in the liquid of unknown refractive index.
View SolutionIn a tank filled with a liquid of refractive index 5/3, a point source of light is placed 2m below the surface of water. To cut off all light coming out of water from the source, what should be the minimum diameter of a disc, which should be placed over the source on the surface of water ?
View Solution
Knowledge Check
A horizontal cylinderical tank 6πm in diameter is half full of water. The space above the water is filled with a pressurized gas of unknown refractive index. A small laser can move along the curved bottom of the water and aims a light beam towards the centre of the water surface. When the laser has moved a distance s=1m or more (measured from curved face) from the lowest point in water, no light enters the gas. The refractive index of gas is (μwater=4/3)
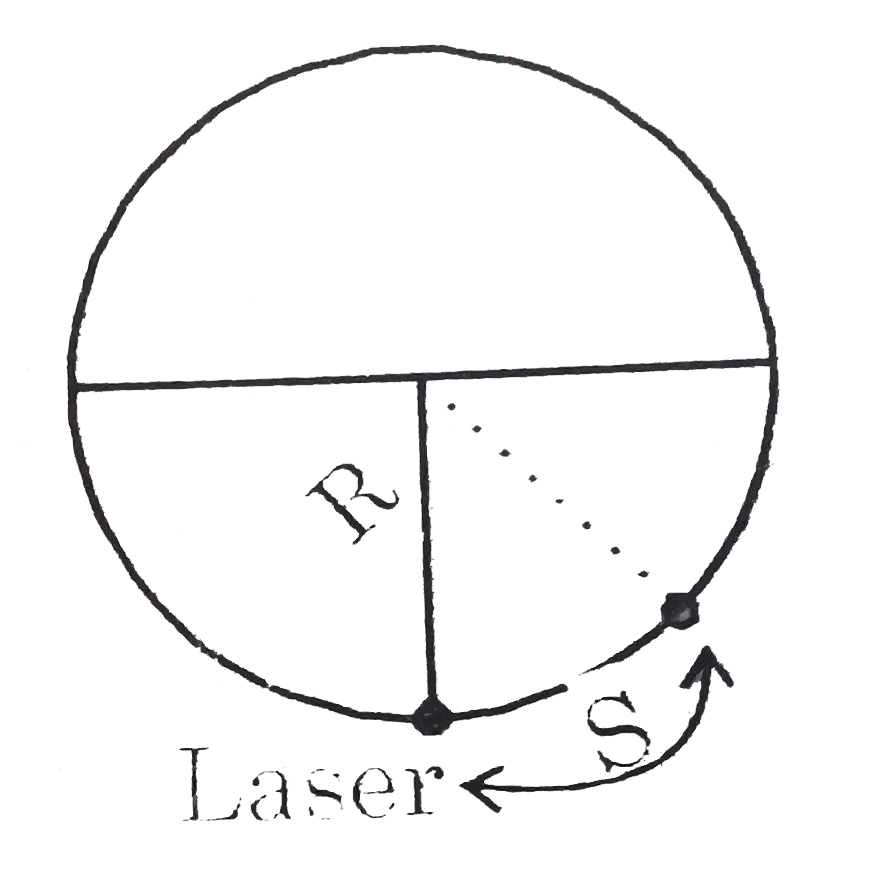 A4/√3B√5/2C2/√3D√3
A4/√3B√5/2C2/√3D√3The refractive index of water is 4/3. The speed of light in water is
A1.50×108m/sB1.78×108m/sC2.25×108m/sD2.67×108m/sA vessel is half filled with a liquid of refractive index μ. The other half of the vessel is filled with an immiscible liquid of refractive index 1.5μ. The apparent depth of vessel is 50% of the actual depth. The value of μ is
A1.6B1.67C1.5D1.4
A point source is placed at a depth h below the surface of water (refractive index =μ). The medium above the surface of water is air from water.
View SolutionA disc is placed on the surface of pond filled with liquid of refractive index 53. A source of light is placed 4m below the surface of liquid. Calculate the minimum area of the disc so that light does not come out of liquid.
View SolutionConsider a tank made of glass (refractive index 1.5) with a thick bottom. It is filled with a liquid of refractive index μ. A student finds that, irrespective of what the incident angle I (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of μ is :

View SolutionA ray of light propagates from glass (refractive index =32) to water (refractive index =43). The value of the critical angel is
View SolutionA poing source of light at the surface of a sphere causes a paralel beam of light to emerge from the opposite surface of the sphere. The refractive index of the material of the sphere is
View Solution