Figure. represents a cuboid. The lengths of the edge, AE, EF and FG are indicated as l, b and h respectively. Indicated the lengths of all other edges.
To find the lengths of all the edges of the cuboid given the lengths of edges AE, EF, and FG as l, b, and h respectively, we can follow these steps:
1. Identify the Given Edges:
- The lengths of the edges are given as:
- AE=l
- EF=b
- FG=h
2. Understand the Structure of a Cuboid:
- A cuboid has 12 edges, and opposite edges are equal in length.
- The edges can be grouped based on their positions:
- Edges parallel to AE and FG are equal.
- Edges parallel to EF are equal.
3. Determine the Lengths of the Opposite Edges:
- The opposite edge to AE is BF, so:
- BF=AE=l
- The opposite edge to EF is AB, so:
- AB=EF=b
- The opposite edge to FG is BC, so:
- BC=FG=h
4. List All Edge Lengths:
- Now, we can list all the edges of the cuboid:
- AE=l
- BF=l
- EF=b
- AB=b
- FG=h
- BC=h
- CD=l (opposite to AE)
- DH=l (opposite to BF)
- EH=b (opposite to AB)
- CG=b (opposite to EF)
- GH=h (opposite to FG)
- HF=h (opposite to BC)
5. Final Summary of Edge Lengths:
- Therefore, the lengths of all edges of the cuboid are:
- AE=l
- BF=l
- EF=b
- AB=b
- FG=h
- BC=h
- CD=l
- DH=l
- EH=b
- CG=b
- GH=h
- HF=h
- The lengths of the edges are given as:
- AE=l
- EF=b
- FG=h
- A cuboid has 12 edges, and opposite edges are equal in length.
- The edges can be grouped based on their positions:
- Edges parallel to AE and FG are equal.
- Edges parallel to EF are equal.
- The opposite edge to AE is BF, so:
- BF=AE=l
- The opposite edge to EF is AB, so:
- AB=EF=b
- The opposite edge to FG is BC, so:
- BC=FG=h
- Now, we can list all the edges of the cuboid:
- AE=l
- BF=l
- EF=b
- AB=b
- FG=h
- BC=h
- CD=l (opposite to AE)
- DH=l (opposite to BF)
- EH=b (opposite to AB)
- CG=b (opposite to EF)
- GH=h (opposite to FG)
- HF=h (opposite to BC)
- Therefore, the lengths of all edges of the cuboid are:
- AE=l
- BF=l
- EF=b
- AB=b
- FG=h
- BC=h
- CD=l
- DH=l
- EH=b
- CG=b
- GH=h
- HF=h
Topper's Solved these Questions
Similar Questions
Figure. represents a cuboid. The lengths of the edge, AE, EF and FG are indicated as l, b and h respectively. Indicated the lengths of all other edges.
View SolutionIn ABC, D, E and F are, respectively, the mid-points of BC, CA and AB . If the lengths of side AB, BC and CA are 7cm, 8cm, and 9cm, respectively, find the perimeter of DEF
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
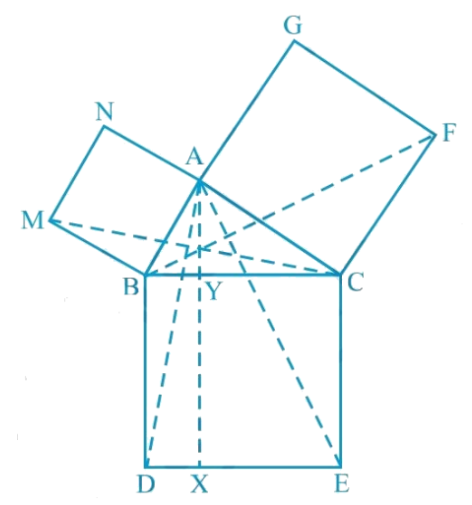
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
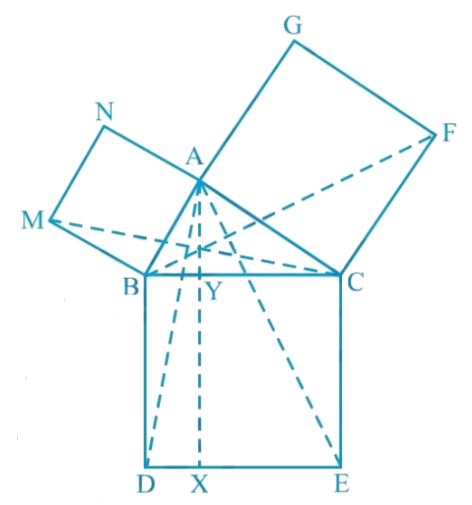
View SolutionIn Figure, triangle ABC is right-angled at B. Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
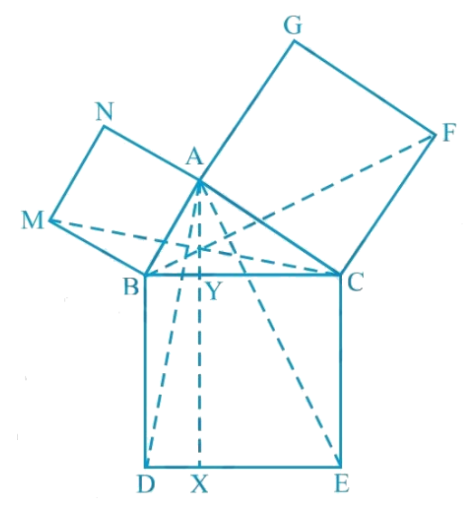
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)=2ar( FCB)
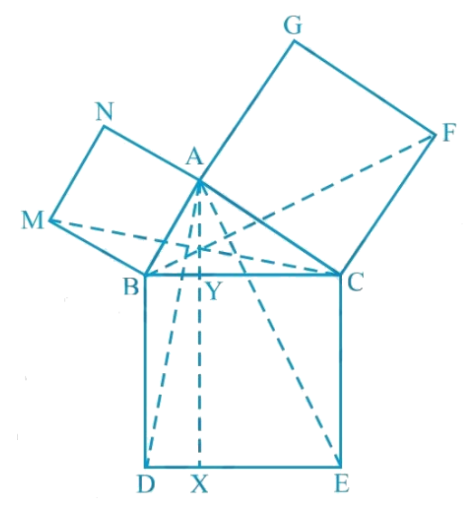
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionABCD is a trapezium with parallel sides AB=a and DC=b. If EandF are mid-points of non-parallel sides ADandBC respectively, then the ratio of areas of quadrilaterals ABFEandEFCD is:
(a) a:b
(b) (a+3b):(3a+b)
(c) (3a+b):(a+3b)
(d) (3a+b):(3a+b)
View SolutionABC is a triangle in which D is the mid-point of BC ,E andF are mid-points of DC and AE respectively. If area of ABC is 16cm2, find the area of DEF
View Solution
