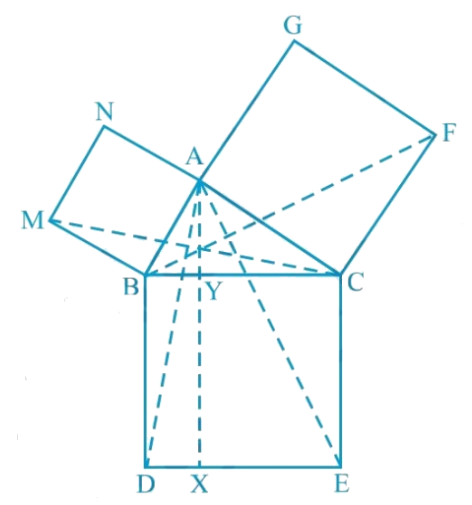
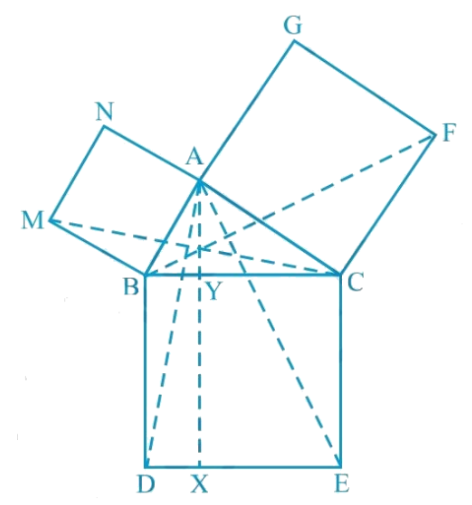
In Figure, ABC
is a right
triangle right angled at A, BCED, ACFG and AMN
are square
on the sides BC, CA and AB
respectively. Line segment AX ⊥DE
meets BC
at Y.
Show that:
ar (CYXE)=2ar( FCB)
Step by step video & image solution for In Figure, A B C is a right triangle right angled at A ,\ B C E D ,\ A C F G\ a n d\ A M N are square on the sides B C ,\ C A\ a n d\ A B respectively. Line segment A X\ _|_D E meets B C at Ydot Show that: a r\ (C Y X E)=2a r(\ F C B) by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
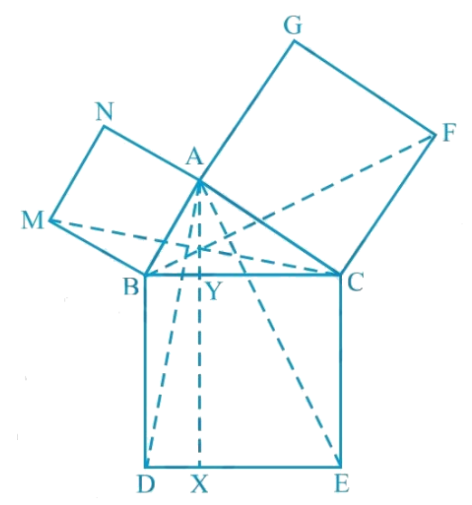
In Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (CYXE)= ar (ACFG)
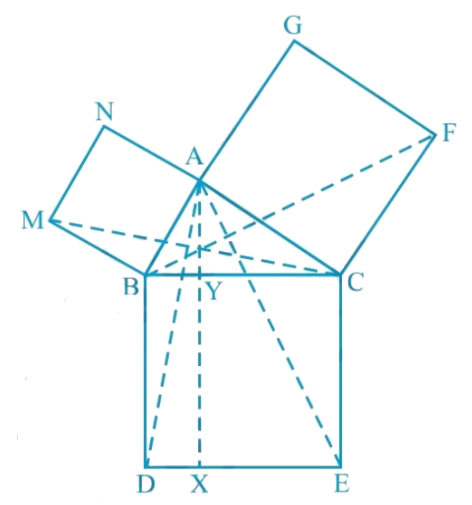
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: FCB≅ ACE
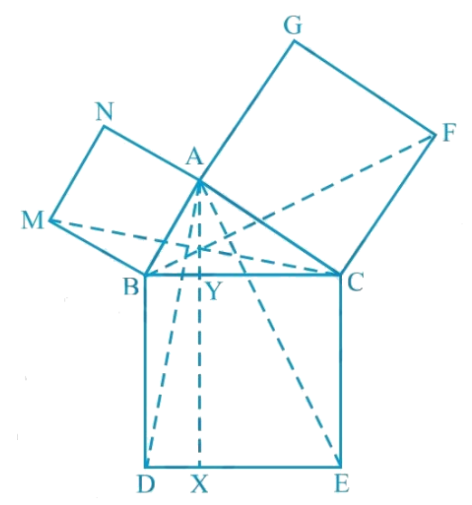
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar(CYXE)=ar (ACFG)
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=2 ar ( MBC)
View SolutionIn Figure, ABC is a right triangle right angled at A, BCED, ACFG and AMN are square on the sides BC, CA and AB respectively. Line segment AX ⊥DE meets BC at Y. Show that: ar (BYXD)=ar (ABMN)
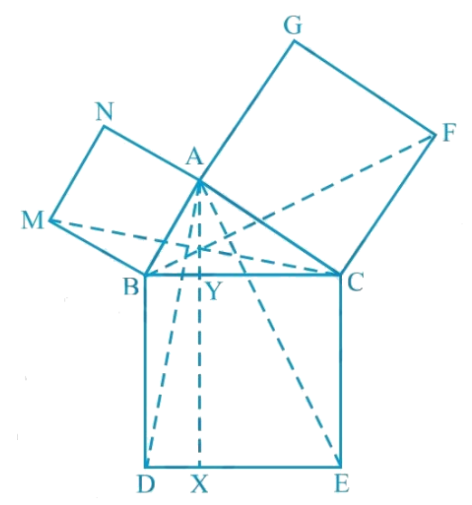
View SolutionABC is a right triangle right angled at A. BCED, ACFG and ABMN aresquares on the sides BC, CA and AB respectively. Line segment AX⊥DEmeets BCat Y. Show that:(i) ΔMBC≅ΔABD(ii) a r\ (B Y X D)\ =\ 2\
View SolutionIn Figure, triangle ABC is right-angled at B. Give that AB=9CM, AC=15CM,andD,E are the mid-points of the sides ABandAC respectively, calculate
The length of BC
(ii) The area of ADE
View SolutionLet ABC be an isosceles triangle in which AB=AC If D,E,F be the mid-points of the sides BC, CA and AB respectively, show that the segment AD and EF bisect each other at right angles.
View SolutionIf D,E,F are the mid-points of the sides BC,CAandAB respectively of a triangle ABC, prove by vector method that AreaofDEF=14(areaofABC).
View SolutionIn a ABC,EandF are the mid-points of ACandAB respectively. The altitude AP to BC intersects FE at Q Prove that AQ=QP
View Solution