In a “magic square”, the sum of the numbers in each row, in each column and along the diagonal is the same. Is this a magic square? TABLE
Step by step video & image solution for In a “magic square”, the sum of the numbers in each row, in each column and along the diagonal is the same. Is this a magic square? TABLE by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In a magic square, the sum of the numbers in each row, in each column and along the diagonals is the same. Is this a magic square?
View SolutionFill in the blank space of the following magic square so that the sum of the numbers in each row, each column and each of the diagonals is – 6.
(i)
In this magic square, sum of the numbers in every row, column and each of the diagonals is – 2. Fill in the blank:

View Solution
Knowledge Check
In a 4×4 matrix the sum of each row, column and both the main diagonals is α. Then the sum of the four corner elements
Ais also αBmay not be αCis never equal to αDnone of these
Complete the magic square given below, so that the sum of the number in each row or in each column or along each diagonal is 15
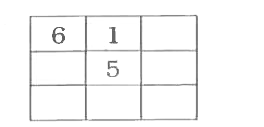
View SolutionComplete the magic square

View SolutionEXAMPLE 3 A magic square is an array of numbers having the same number of rows and columns and the sum of the numbers in a row column and the sum of the numbers in each row column or diagonal being the same. Fill in the blank cells of the following magic square.
View SolutionIn a magic square each row, column and diagonal have the same sum. Check which of the following is a magic square.
View SolutionIn a magic square, each row.column and diagonal have the same sum. Check which of the following is a magic square.
View SolutionIn a magic square each row, column and diagonal have the same sum , then the values of A and B are
View SolutionIn a 4×4 matrix, the sum of every row, every column and both the diagonals is 10 each, then the sum of 4 corner elements is λ. Then λ is divisible by
View Solution