In Fig. 64, AB∣∣CD and a transversal PQ cuts them at L and M respectively. If ∠QMD=1000, find all other angles.
To solve the problem step by step, we will use the properties of parallel lines and transversals.
Given:
- AB∥CD
- Transversal PQ cuts AB at point L and CD at point M
- ∠QMD=100∘
To Find:
All other angles formed by the transversal and the parallel lines.
1. Identify the Angles:
- We have ∠QMD=100∘.
- We need to find ∠QMC, ∠PLB, ∠PLA, and ∠LMC.
2. Use Linear Pair Property:
- Angles QMD and QMC are a linear pair (they form a straight line).
- Therefore, ∠QMD+∠QMC=180∘.
- Substitute ∠QMD=100∘:
100∘+∠QMC=180∘
- Rearranging gives:
∠QMC=180∘−100∘=80∘
3. Use Vertical Angles Property:
- Angles QMD and PLB are vertical angles.
- Therefore, ∠PLB=∠QMD=100∘.
4. Use Vertical Angles Property Again:
- Angles QMC and PLA are also vertical angles.
- Therefore, ∠PLA=∠QMC=80∘.
5. Use Alternate Interior Angles Property:
- Angles LMC and PLB are alternate interior angles.
- Therefore, ∠LMC=∠PLB=100∘.
6. Use Alternate Interior Angles Property Again:
- Angles LMC and QMC are also alternate interior angles.
- Therefore, ∠LMC=∠QMC=80∘.
Summary of Angles:
- ∠QMD=100∘
- ∠QMC=80∘
- ∠PLB=100∘
- ∠PLA=80∘
- ∠LMC=100∘
Final Answer:
- ∠QMD=100∘
- ∠QMC=80∘
- ∠PLB=100∘
- ∠PLA=80∘
- ∠LMC=100∘
- AB∥CD
- Transversal PQ cuts AB at point L and CD at point M
- ∠QMD=100∘
All other angles formed by the transversal and the parallel lines.
- We have ∠QMD=100∘.
- We need to find ∠QMC, ∠PLB, ∠PLA, and ∠LMC.
- Angles QMD and QMC are a linear pair (they form a straight line).
- Therefore, ∠QMD+∠QMC=180∘.
- Substitute ∠QMD=100∘:
100∘+∠QMC=180∘
- Rearranging gives:
∠QMC=180∘−100∘=80∘
- Angles QMD and PLB are vertical angles.
- Therefore, ∠PLB=∠QMD=100∘.
- Angles QMC and PLA are also vertical angles.
- Therefore, ∠PLA=∠QMC=80∘.
- Angles LMC and PLB are alternate interior angles.
- Therefore, ∠LMC=∠PLB=100∘.
- Angles LMC and QMC are also alternate interior angles.
- Therefore, ∠LMC=∠QMC=80∘.
- ∠QMD=100∘
- ∠QMC=80∘
- ∠PLB=100∘
- ∠PLA=80∘
- ∠LMC=100∘
- ∠QMD=100∘
- ∠QMC=80∘
- ∠PLB=100∘
- ∠PLA=80∘
- ∠LMC=100∘
Topper's Solved these Questions
Similar Questions
In Fig. 63, line l ∣∣ m and a transversal n cuts them at P and Q respectively. If ∠1=750, find all other angles.
View SolutionIn Fig.59, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively, If ∠CMQ=600 find all other angles in the figure.
View SolutionIn Fig. 60, AB and CD are parallel lines intersected by a transversal PQ at L and M respectively. If ∠LMD=350 find ∠PLA.
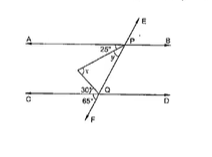
View SolutionIn Figure, AB and CD are parallel lines and transversal EF intersects them at P and Q respectively. If ∠APR=250, ∠RQC=300and ∠CQF=650, then x=550, y=440 (b) x=550, y=450 x=600, y=350 (d) x=350, y=600
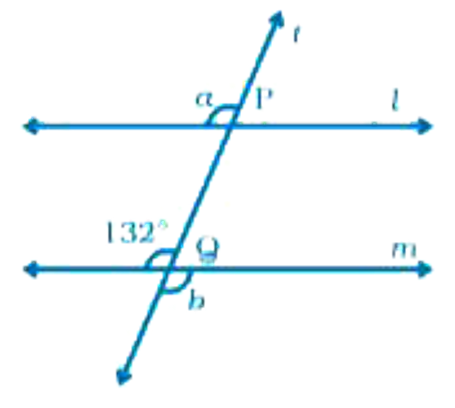
View SolutionIn Fig. 5.55, l ||m and a line t intersects these lines at P and Q, respectively. Find the sum 2a + b.
View SolutionIn Fig.100, ABCD and EF is a transversal intersecting AB and CD at P and Q respectively. The measure of ∠DOP is (a) 65 (b) 25 (c) 115 (d) 105
View SolutionIn Fig.99, ABCD and EF is a transversal intersecting AB and CD at P and Q respectively. The measure of ∠DPQ is (a) (b)(c)(d)(e)100(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)80(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)110(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)70(q)0(r)(s)(t) (u)
View SolutionIn Fig. 73, a transversal n cuts two lines l and m.if ∠1=700 and ∠7=800, is lm?
View SolutionIn Fig. 62, line l∣∣m and n is a transversal. If ∠1=400, find all the angles and check that all corresponding angles and alternate angles are equal.
View SolutionIn Fig. 74, a transversal n cuts two lines l and m such that ∠2=650 and ∠8=650. Are the lines parallel?
View Solution
