The sides BC,CA and AB of a triangle ABC, are produced in order, forming exterior angles ∠ACD,∠BAE and ∠CBF . Show that ∠ACD+∠BAE+∠CBF=3600
Step by step video solution for The sides B C ,C A and A B of a triangle A B C , are produced in order, forming exterior angles /_A C D ,/_B A E and /_C B F . Show that /_A C D+/_B A E+/_C B F=360^0 by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
(Exterior Angle Theorem): If a side of a triangle is produced, the exterior angle so formed is equal to the sum of the two interior opposite angles. GIVEN : A triangle ABC.D is a point of BC produced, forming exterior angle ∠4. TO PROVE : ∠4=∠1+∠2 i.e. , ∠ACD=∠CAB+∠CBA.
View SolutionIf ABCD is a rhombus with ∠ABC=56∘, find the measure of ∠ACD
View Solution
Knowledge Check
∠A,∠B,∠Care three angles of a triangle. If ∠A−∠B=15∘,∠B−∠C=30∘, then ∠A,∠Band∠C are
A80∘,60∘,40∘B70∘,50∘,60∘C80∘,65∘,35∘D80∘,55∘,45∘In a Δ ABC, if 2∠A=3∠B=6∠C then calculate ∠A,∠B and ∠C.
A∠A=40∘,∠B=60∘ and ∠C=30∘B∠A=60∘,∠B=60∘ and ∠C=30∘C∠A=90∘,∠B=60∘ and ∠C=30∘D∠A=90∘,∠B=90∘ and ∠C=30∘
If the sides of a triangle are produced in order, then the sum of the three exterior angles so formed is 900 (b) 1800 (c) 2700 (d) 3600
View SolutionTwo triangles ABC and DEF such that ∠A=∠D,∠B=∠Eand∠C=∠F. Then
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
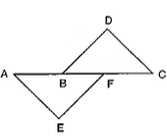
View SolutionAny point D is taken in the base BC of a triangle ABC and AD is produced to E, making DE equal to AD. Show that ar (BCE)=ar(ABC)
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
View SolutionIn fig.41, ABC is a right triangle right angled at A. D lies on BA produced and DE⊥BC, intersecting AC at F . if ∠AFE=1300, find ∠BDE (ii) ∠BCA ∠ABC
View Solution
