Triangles ABC and DBC have side BC common, AB=BD and AC=CD. Are the two triangles congruent? State in symbolic form. Which congruence condition do you use? Does △ABD equal △ACD? Why or why not?
Step by step video & image solution for Triangles A B C\ a n d\ D B C\ have side B C common, A B=B D\ a n d\ A C=C Ddot Are the two triangles congruent? State in symbolic form. Which congruence condition do you use? Does\ /_\ A B D\ e q u a l\ /_\ A C D ? Why or why not? by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Fig.85, ABCD and ACBD. Find the value of x,y,z.
View SolutionΔ ABC and Δ ABD are on a common base AB, and AC = BD and BC = AD as shown in Fig. 18. Which of the following statements is true? ΔABC≅ΔABD ΔABC≅ΔADB ΔABC≅ΔBAD
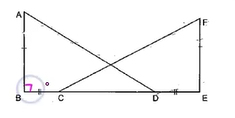
View SolutionIn Figure, AB⊥BEandFE⊥BE.If BC=DEandAB=EF, then ABD is congruent to:
(a)EFC
(b) ECF
(c) CEF
(d) FEC
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionIn triangles ABC and PQR, if ∠A=∠R, ∠B=∠P and AB=RP , then which one of the following congruence conditions applies:
(a) SAS
(b) ASA
(c) SSS
(d) RHS
View SolutionABCD is a kite having AB=AD and BC=CD . Prove that the figure formed by joining the mid-points of the sides, in order, is a rectangle.
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).

View SolutionIn Figure, ABCandBDE are two equilateral triangles such that D is the mid-point of BC,AE intersects BC in F
Prove that: ar(BDE)=14ar(ABC)
View SolutionIn Fig.31, AB=AD and ∠BAC=∠DAC State in symbolic form the congruence of two triangles ABC and ADC that is true. Complete each of the following, so as to make it true: △ABC △ACD Line segment bisects ____ and _____
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View Solution
