Δ ABC and Δ ABD are on a common base AB, and AC = BD and BC = AD as shown in Fig. 18. Which of the following statements is true? ΔABC≅ΔABD ΔABC≅ΔADB ΔABC≅ΔBAD
To determine which of the statements about triangles ΔABC and ΔABD is true, we will analyze the given information step by step.
1. Identify the Common Base:
Both triangles ΔABC and ΔABD share a common base, which is line segment AB.
Hint: Look for segments that both triangles have in common.
2. Given Lengths:
We know that AC=BD and BC=AD. This means that the lengths of sides opposite to the common base are equal.
Hint: Identify the corresponding sides of both triangles that are given to be equal.
3. Apply the Criteria for Congruence:
We can use the Side-Side-Side (SSS) congruence criterion. According to this criterion, if three sides of one triangle are equal to three sides of another triangle, then the two triangles are congruent.
- For ΔABC:
- Side 1: AB (common base)
- Side 2: AC
- Side 3: BC
- For ΔABD:
- Side 1: AB (common base)
- Side 2: AD
- Side 3: BD
We know:
- AB=AB (common side)
- AC=BD
- BC=AD
Therefore, we can conclude that:
ΔABC≅ΔABD
Hint: Remember that congruence means all corresponding sides are equal.
4. Conclusion:
Since we have established that all corresponding sides are equal, the correct statement is:
ΔABC≅ΔABD
Final Answer:
The correct statement is ΔABC≅ΔABD.
Both triangles ΔABC and ΔABD share a common base, which is line segment AB.
We know that AC=BD and BC=AD. This means that the lengths of sides opposite to the common base are equal.
We can use the Side-Side-Side (SSS) congruence criterion. According to this criterion, if three sides of one triangle are equal to three sides of another triangle, then the two triangles are congruent.
- Side 1: AB (common base)
- Side 2: AC
- Side 3: BC
- Side 1: AB (common base)
- Side 2: AD
- Side 3: BD
- AB=AB (common side)
- AC=BD
- BC=AD
ΔABC≅ΔABD
Since we have established that all corresponding sides are equal, the correct statement is:
ΔABC≅ΔABD
The correct statement is ΔABC≅ΔABD.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If a, b, c, d and e are positve numbers, and it is given that ,
a+b=c+db+d=2ad+e>a+bandc+d>a+e
then, which of the following statement is true ?Ad>a>b>e>cBd>b>e>a>cCa>b>c>d>eDa>d>b>e>c
ΔABCand ΔDBCare two isosceles triangles on the same base BC and vertices A and D are on the same side of BC (see Fig. 7.39). If AD is extended to intersect BC at P, show that (i) ΔABD≅ΔACD
(ii) ΔABP≅ΔACP
(iii) AP bisects ∠A as well as ∠D
(iv) AP is the perpendicular bisector of BC

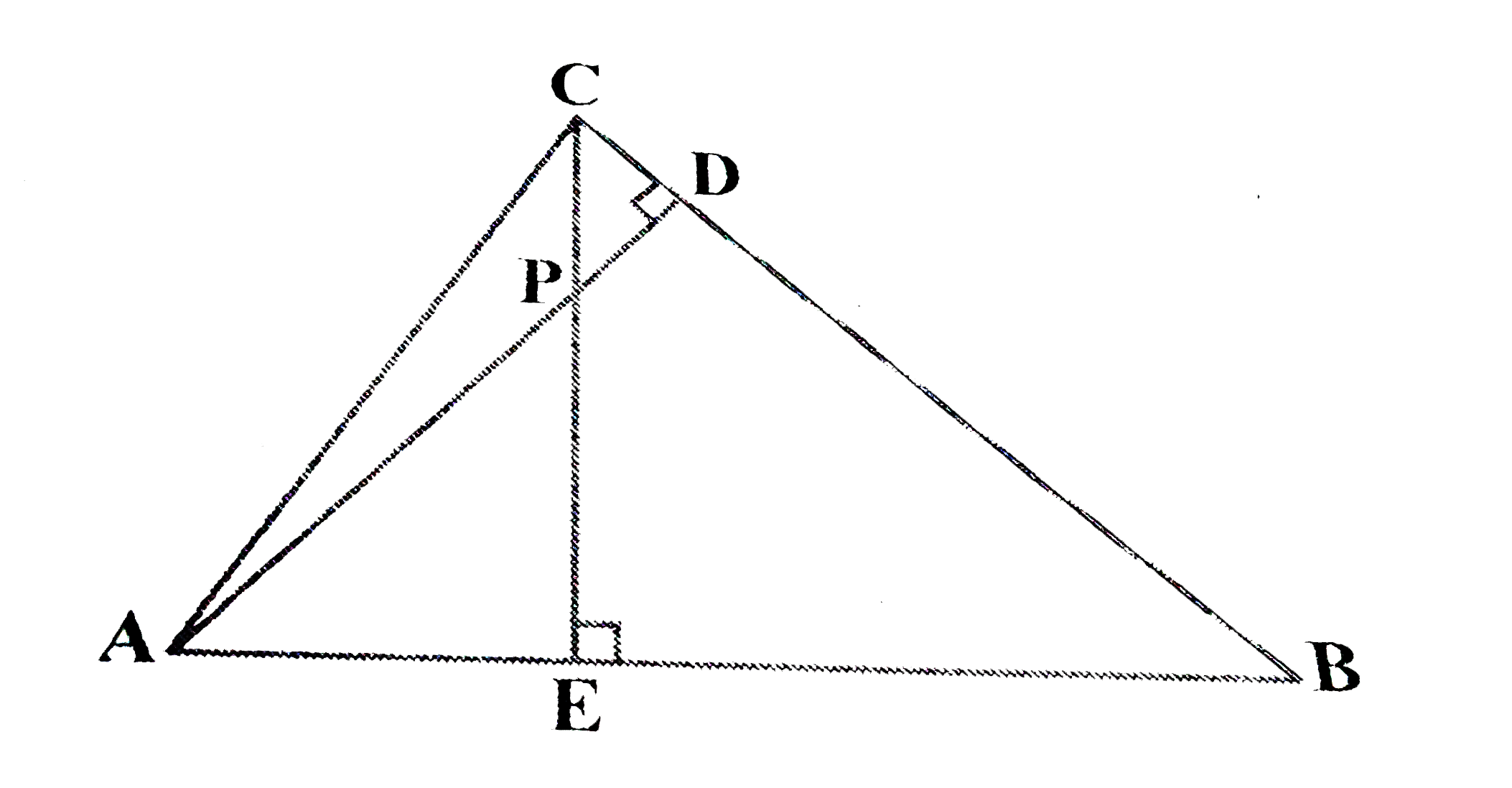
View SolutionIn Figure altitudes AD and CE of DABC intersect each other at the point P. Show that:
(i) ΔAEP~ΔCDP
(ii) ΔABD~ΔCBE
(iii) ΔAEP~ΔADB
(iv) ΔPDC~ΔBEC
View SolutionIn square ABCD, P and Q are mid-point of AB and CD respectively. If AB=8cm and PQ and BD intersect at O, then find area of OPB
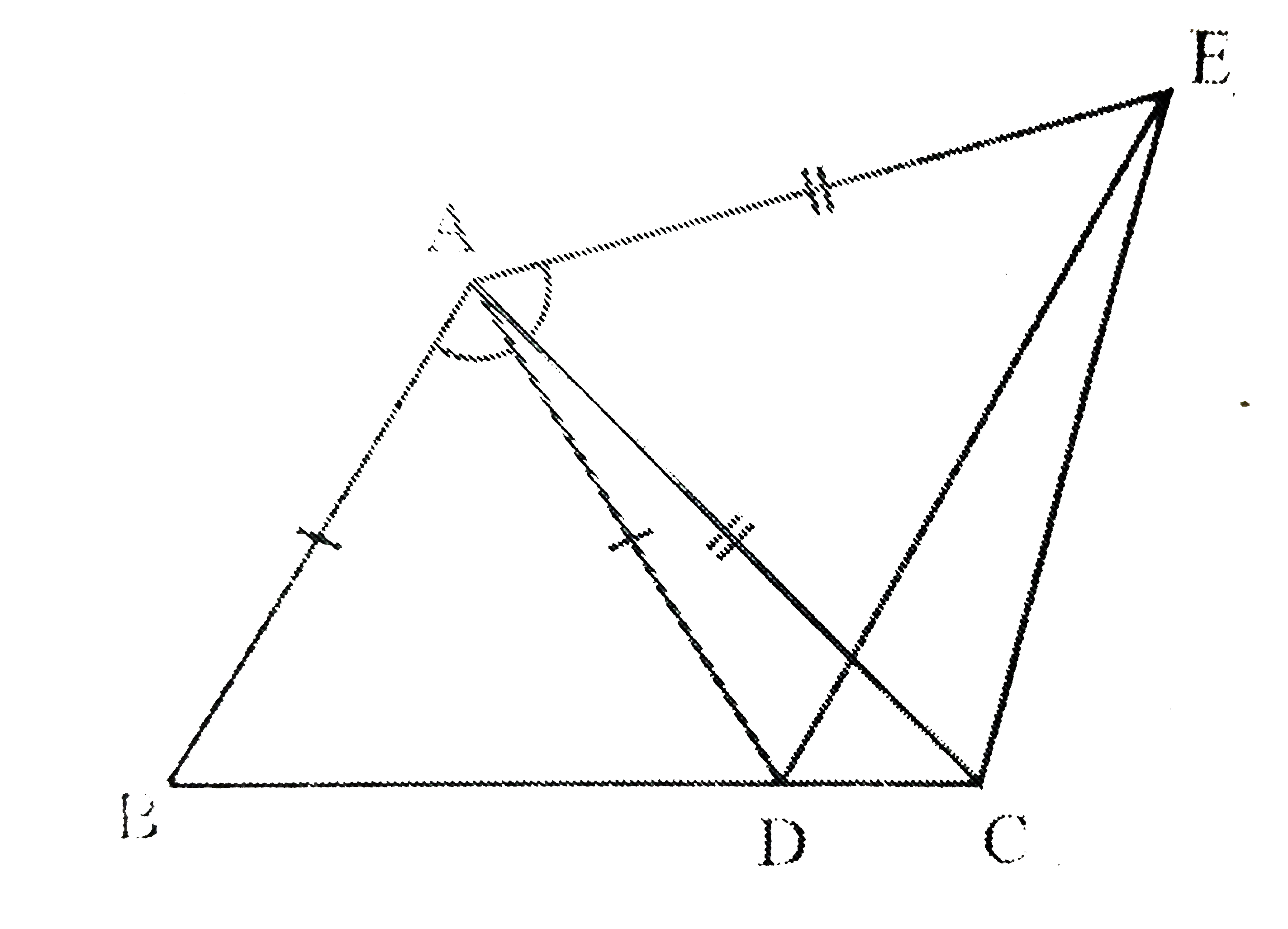
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionIn a parallelogram ABCD diagonals AC and BD intersect at O and AC=6.8 cm and BD=5.6cm . Find the measures of OC and OD
View SolutionAB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View Solution

