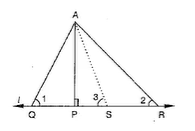
In Fig.44, it is given that LM=MN, QM=MR, ML⊥PQ and MN⊥PR. Prove that PQ=PR.
To prove that PQ=PR given the conditions LM=MN, QM=MR, ML⊥PQ, and MN⊥PR, we can follow these steps:
Step 1: Identify the triangles
We will consider two triangles, △MLQ and △MNR.
Step 2: Establish the right angles
From the problem statement, we know that:
- ML⊥PQ implies ∠MLQ=90∘
- MN⊥PR implies ∠MNR=90∘
Step 3: Identify the sides
We have:
- LM=MN (given)
- QM=MR (given)
Step 4: Apply the RHS congruence criterion
Now we can apply the RHS (Right angle-Hypotenuse-Side) congruence criterion to triangles △MLQ and △MNR:
- Both triangles have a right angle (90∘).
- The hypotenuses MQ and MR are equal because QM=MR.
- The sides LM and MN are equal.
Step 5: Conclude the congruence of triangles
By RHS, we conclude that:
△MLQ≅△MNR
Step 6: Corresponding parts of congruent triangles
Since the triangles are congruent, the corresponding parts are equal:
QL=NR
Step 7: Establish the relationship between PQ and PR
Now, we can express PQ and PR in terms of the segments we have established:
PQ=PL+QL
PR=PN+NR
Step 8: Show that PQ=PR
Since QL=NR (from the congruence of triangles), we can substitute:
PQ=PL+NR
PR=PN+NR
Now, if we can show that PL=PN, we can conclude:
PQ=PR
Step 9: Establish PL=PN
Using the congruence of triangles △MLQ and △MNR, we can show that:
- PL corresponds to PN in the congruent triangles.
Thus, we conclude:
PQ=PR
Final Conclusion
Therefore, we have proved that PQ=PR.
---
We will consider two triangles, △MLQ and △MNR.
From the problem statement, we know that:
- ML⊥PQ implies ∠MLQ=90∘
- MN⊥PR implies ∠MNR=90∘
We have:
- LM=MN (given)
- QM=MR (given)
Now we can apply the RHS (Right angle-Hypotenuse-Side) congruence criterion to triangles △MLQ and △MNR:
- Both triangles have a right angle (90∘).
- The hypotenuses MQ and MR are equal because QM=MR.
- The sides LM and MN are equal.
By RHS, we conclude that:
△MLQ≅△MNR
Since the triangles are congruent, the corresponding parts are equal:
QL=NR
Now, we can express PQ and PR in terms of the segments we have established:
PQ=PL+QL
PR=PN+NR
Since QL=NR (from the congruence of triangles), we can substitute:
PQ=PL+NR
PR=PN+NR
PQ=PR
Using the congruence of triangles △MLQ and △MNR, we can show that:
- PL corresponds to PN in the congruent triangles.
PQ=PR
Therefore, we have proved that PQ=PR.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If L=+,M=−,N=×,P=÷, then 5N5P5L5M5=?
A0B5C10D15
In PQR , M and N are points on sides PQ and PR respectively such that PM=15cm and NR=8cm . If PQ=25cm and PR=20cm state whether MNQR .
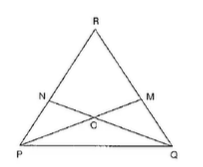
View SolutionIn Figure, ∠QPR= ∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN. Prove that OP=OQ, where O is the point of intersection of PM and QN
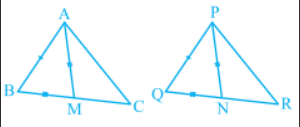
View SolutionIn Figure, two sides AB and BC and the median AD of ABC are equal respectively to the two sides PQ and QR and the median PM of the other triangle PQR. Prove that ABD≅PQM (ii) ABC ≅ PQR
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
View SolutionIn Fig. 6.24, if PQ∣∣RS,∠MXQ=135∘ and∠MYR=40∘, find∠XMY..

View SolutionIn Figure, PQRS is a parallelogram, PO and QO are, respectively, the angle bisectors of ∠P and ∠Q . Line LOM is drawn parallel to PQ . Prove that: PL=QM (ii) LO=OM
View SolutionIn Figure, ∠QPR=∠PQR and M and N are respectively on sides QR and PR of PQR such that QM=PN . Prove that OP=OQ, where O is the point of intersection of PM and QN.

View Solution