Describe the graph of the set of points (x,y,z) where x2+z2=1.
Since y is not in the equation . It can take any value , when restricted to the xz plane , the equation is that of a circle with radius 1 and the center at the origin ,Therefore in xyz space , the equation represents a cylindrical shape , centered at the origin , that extends indefinitely in both directions along the y- axis .
A solid figure can also be obtained by rotating a plane figure about some line in the plane that does not intersect the figure .
Topper's Solved these Questions
- BOOK - ENGLISH SATCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - EXERCISE6videos
THREE DIMENSIONAL GEOMETRY
- BOOK - ENGLISH SATCHAPTER - STRATEGIES FOR SOLVING SAT MATH PROBLEMS EXERCISE - EXAMPLE19videos
STRATEGIES FOR SOLVING SAT MATH PROBLEMS
- BOOK - ENGLISH SATCHAPTER - TRANSFORMATION AND SYMMETRYEXERCISE - EXERCISES4videos
TRANSFORMATION AND SYMMETRY
Similar Questions
Knowledge Check
- Question 1 - Select One
The set of points (x,y,z) such that x=5 is
Aa pointBa lineCa planeDa circle - Question 2 - Select One
If (x,y) represents a point on the the graph of y=2x+1, which of the following could be a portion of the graph of the set of points (x,y2)?
A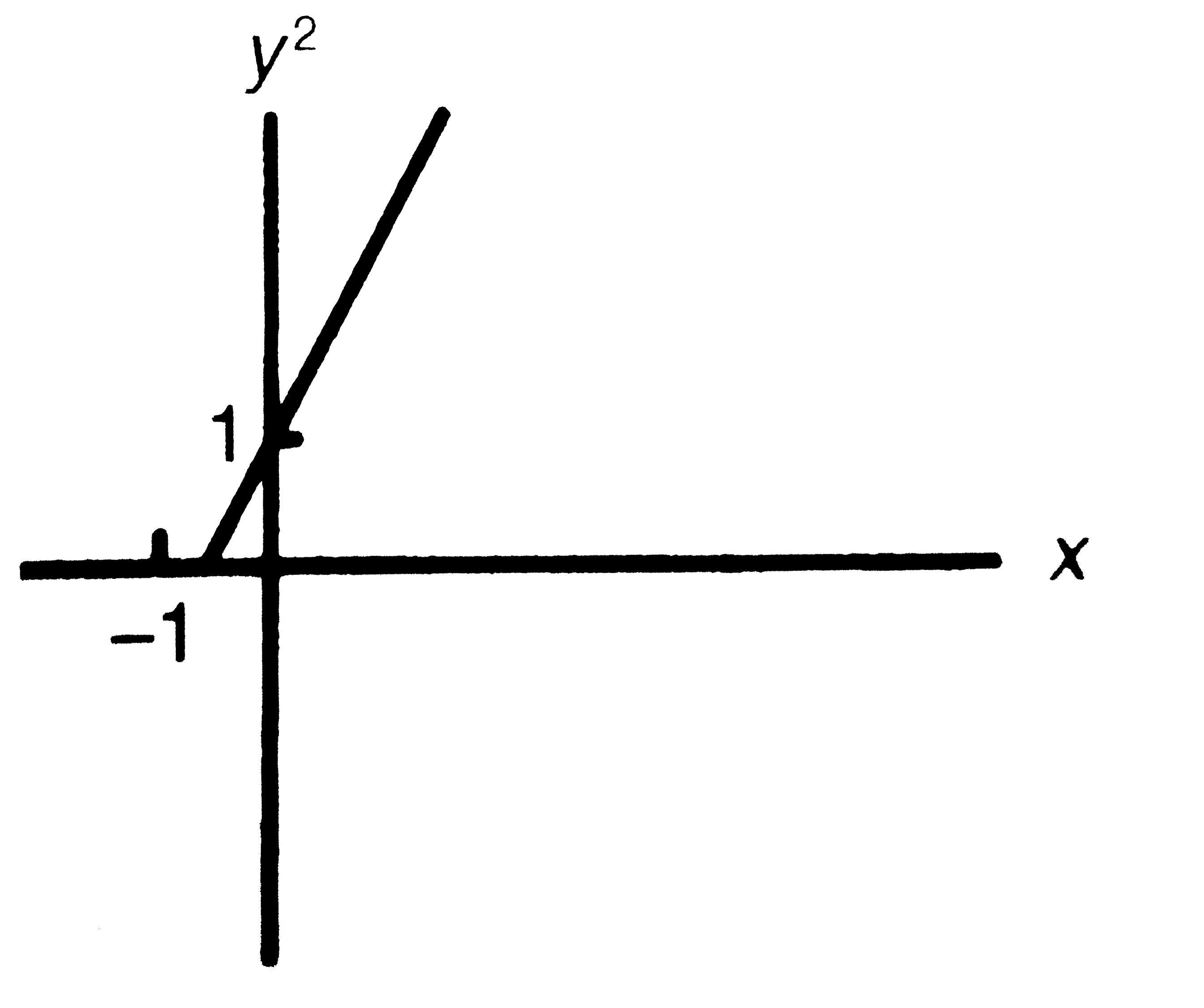 B
B C
C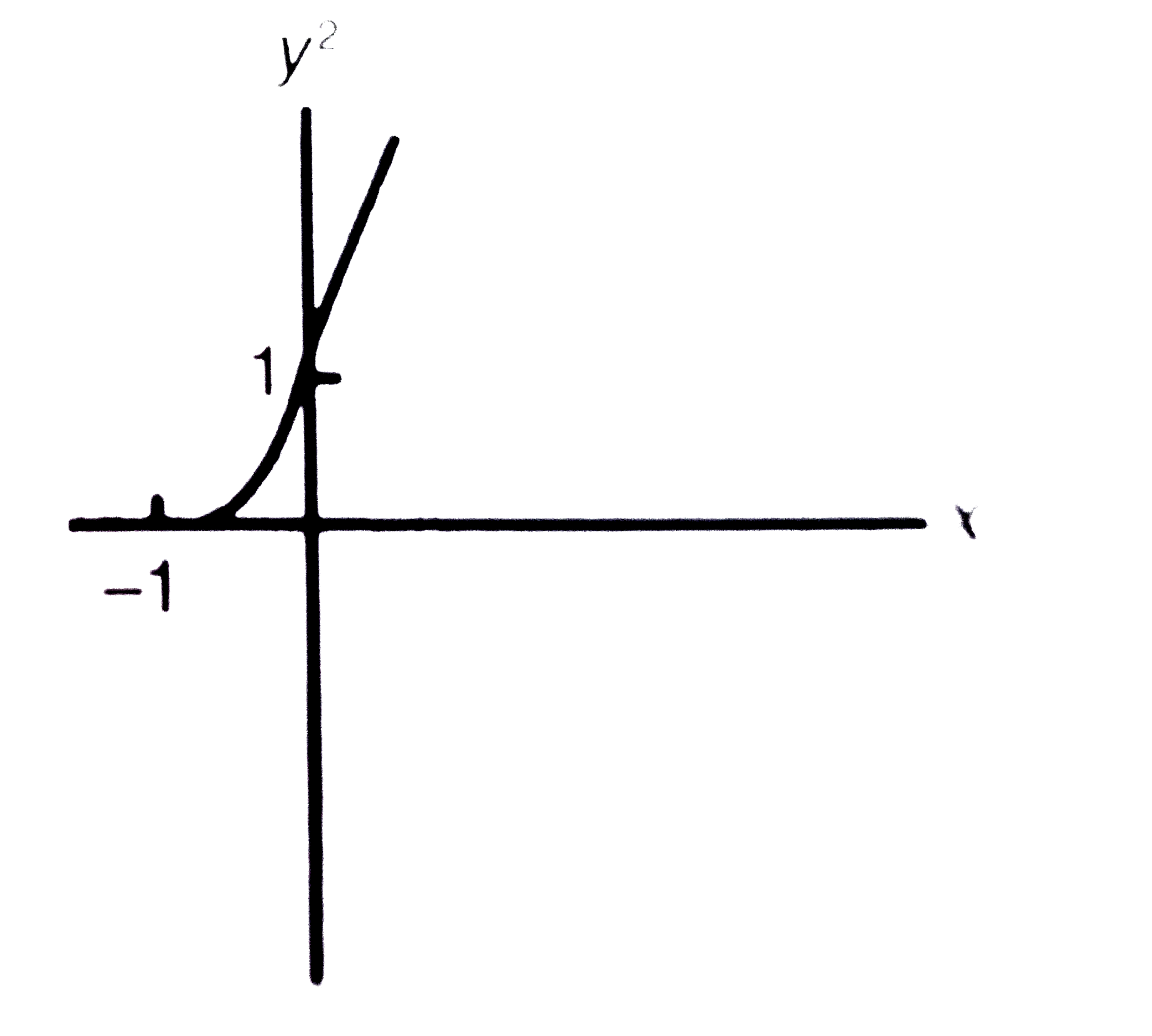 D
D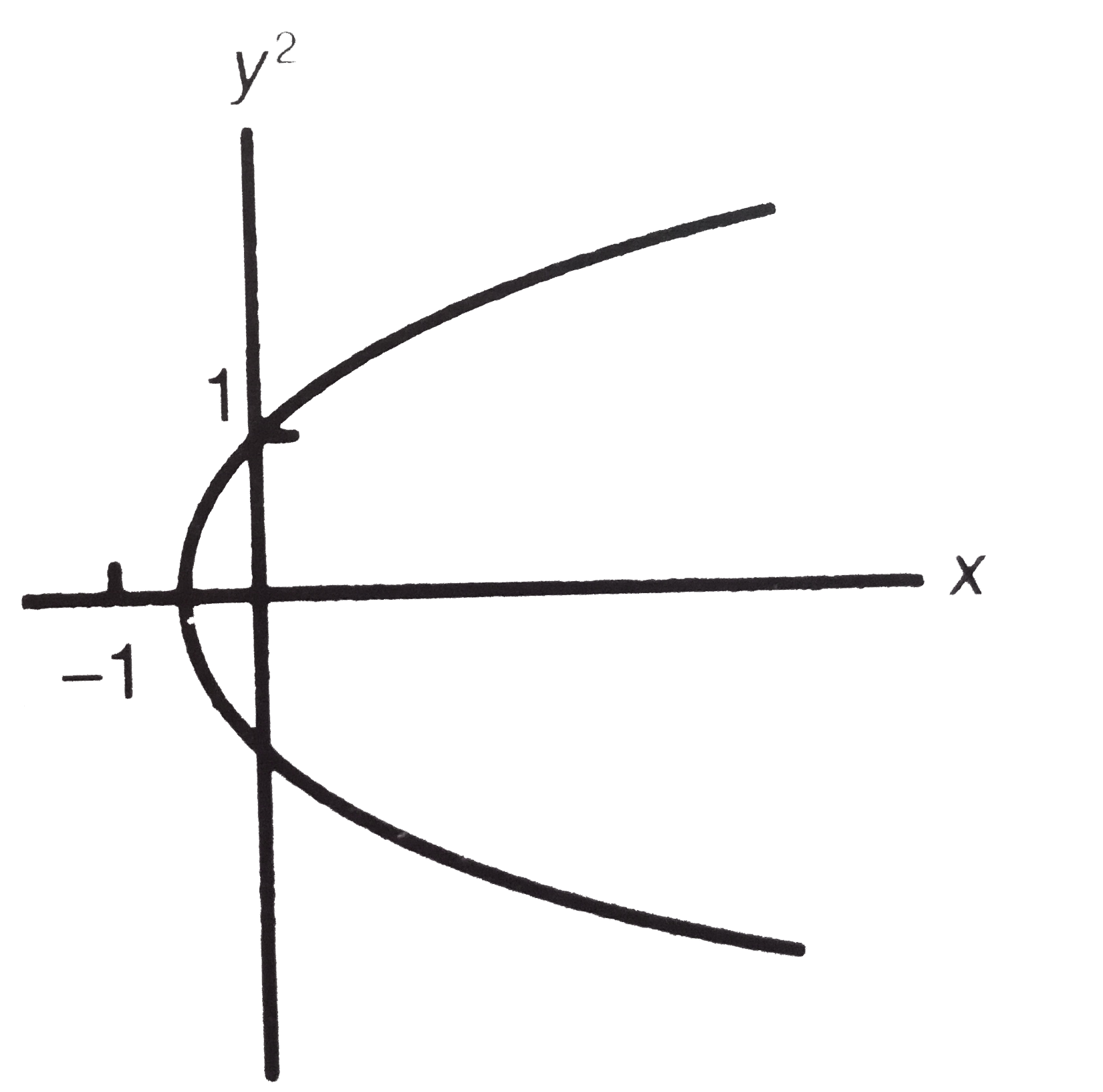
The lines x=y=z meets the plane x+y+z=1 at the point P and the sphere x2+y2+z2=1 at the point R and S, then
View SolutionA plane which passes through the point (3,2,0) nd the line x−41=y−75=z−44 is (A) x−y+z=1 (B) x+y+z=5(C)x+2y-z=1(D)2x-y+z=5
View SolutionFind the number of triplets (x, y, z) of integers satisfying the equations x+y=1−z and x3+y3=1−z2 (where z≠1)
View SolutionThe intersection of the spheres x2+y2+z2+7x−2y−z=13andx2+y2+z2−3x+3y+4z=8 is the same as the intersection of one of the spheres and the plane a. x−y−z=1 b. x−2y−z=1 c. x−y−2z=1 d. 2x−y−z=1
View SolutionThe intersection of the spheres x2+y2+z2+7x−2y−z=13andx2+y2+z2−3x+3y+4z=8 is the same as the intersection of one of the spheres and the plane a. x−y−z=1 b. x−2y−z=1 c. x−y−2z=1 d. 2x−y−z=1
View SolutionThe length of projection of the segment join (x1,y1,z1)and(x2,y2,z20 on te line x−αl=y−βm=z−γn is (A) ∣l(x2−x1)+m(y2−y1)+n(z2−z1) (B) |α(x2−x1)+β(y2−y1)+γ(z2−z1)|(C)|(x_2-x_1)/l+(y_2-y_1)/m+(z_2-z_1)/n| (D) none of these
View Solution

