Observers at locations due north and due south of a rocket launchpad sight a rocket at a height of 10 kilometers. Assume that the curvature of earth is negligible and that the rocket's trajectory at that time is perpendicular to the gound. How far apart are the two observers if their angles of elevation to the rocket are 80.5∘and68.0∘?
0.85 km
4.27 km
5.71 km
20.92 km
The correct Answer is:C
To solve the problem, we need to determine the distance between the two observers based on their angles of elevation to the rocket. Here’s a step-by-step solution:
Step 1: Understand the Problem
We have two observers located due north and due south of a rocket launchpad. The rocket is at a height of 10 kilometers, and the angles of elevation from the observers to the rocket are 80.5 degrees and 68 degrees.
Step 2: Draw a Diagram
Let's denote:
- Point C as the position of the rocket.
- Point A as the position of the observer to the north.
- Point B as the position of the observer to the south.
The height of the rocket (point C) is 10 km. The angles of elevation from points A and B to point C are 80.5 degrees and 68 degrees, respectively.
Step 3: Set Up the Right Triangles
From the observers' points (A and B), we can form two right triangles:
- Triangle AOC (for observer A):
- Opposite side (height of the rocket) = 10 km
- Angle of elevation = 80.5 degrees
- Triangle BOC (for observer B):
- Opposite side (height of the rocket) = 10 km
- Angle of elevation = 68 degrees
Step 4: Use Trigonometric Ratios
Using the tangent function, we can express the distances from the observers to the base of the rocket (points A and B) in terms of the angles of elevation:
1. For observer A:
tan(80.5∘)=10AC
Rearranging gives:
AC=10tan(80.5∘)
2. For observer B:
tan(68∘)=10BC
Rearranging gives:
BC=10tan(68∘)
Step 5: Calculate Distances AC and BC
Now, we can calculate the distances using a calculator:
1. Calculate AC:
AC=10tan(80.5∘)≈105.144≈1.94 km
2. Calculate BC:
BC=10tan(68∘)≈102.475≈4.04 km
Step 6: Find the Total Distance Between Observers A and B
The total distance AB between the two observers is the sum of distances AC and BC:
AB=AC+BC≈1.94+4.04≈5.98 km
Conclusion
The distance between the two observers is approximately 5.98 kilometers.
We have two observers located due north and due south of a rocket launchpad. The rocket is at a height of 10 kilometers, and the angles of elevation from the observers to the rocket are 80.5 degrees and 68 degrees.
Let's denote:
- Point C as the position of the rocket.
- Point A as the position of the observer to the north.
- Point B as the position of the observer to the south.
From the observers' points (A and B), we can form two right triangles:
- Triangle AOC (for observer A):
- Opposite side (height of the rocket) = 10 km
- Angle of elevation = 80.5 degrees
- Triangle BOC (for observer B):
- Opposite side (height of the rocket) = 10 km
- Angle of elevation = 68 degrees
Using the tangent function, we can express the distances from the observers to the base of the rocket (points A and B) in terms of the angles of elevation:
tan(80.5∘)=10AC
Rearranging gives:
AC=10tan(80.5∘)
tan(68∘)=10BC
Rearranging gives:
BC=10tan(68∘)
Now, we can calculate the distances using a calculator:
AC=10tan(80.5∘)≈105.144≈1.94 km
BC=10tan(68∘)≈102.475≈4.04 km
The total distance AB between the two observers is the sum of distances AC and BC:
AB=AC+BC≈1.94+4.04≈5.98 km
The distance between the two observers is approximately 5.98 kilometers.
Topper's Solved these Questions
Similar Questions
An inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00. What should be the initial downward speed of the rocketeer so that he catches the student at the top of 100 the floor for safe landing ?View SolutionAn inquistive student, determined to test the law of gravity for himself, walks to the top of a building og 145 floors, with every floor of height 4 m, having a stopwatch in his hand (the first floor is at a height of 4 m from the ground level). From there he jumps off with negligible speed and hence starts rolling freely. A rocketeer arrives at the scene 5 s later and dives off from the top of the building to save the student. The rocketeer leaves the roof with an initial downward speed v0. In order to catch the student at a sufficiently great height above ground so that the rocketeer and the student slow down and arrive at the ground with zero velocity. The upward acceleration that accomplishes this is provided by rocketeer's jet pack, which he turns on just as he catches the student, before the rocketeer is in free fall. To prevent any discomfort to the student, the magnitude of the acceleration of the rocketeer and the student as they move downward together should not exceed 5 g.
Just as the student starts his free fall, he presses the button of the stopwatch. When he reaches at the top of 100th floor, he has observed the reading of stopwatch as 00:00:06:00 (hh:mm:ss:100 th part of the second). Find the value of g. (correct upt ot two decimal places).View Solution
Knowledge Check
- Question 1 - Select One
A long straight horizontal cable carries a current of 2.5amp. In the direction 10∘ south of west to 10∘ north of east, figure. The magnetic meridian of the place happens to be 10∘ west of the geographic meridian. The earth's magnetic field at the location is 0.33G and the angle of dip is zero. Locate the line of neutral points (Ignore the thickness of the cable). [At neutral points, magnetic fied due to a current cable is equal and opposite to the horizontal component of earth's magnetic field.]
 A15.15mmB30.15mmC35.15mmD40.15mm
A15.15mmB30.15mmC35.15mmD40.15mm
A rocket is receding away from earth with velocity 0.2C. The rocket emits signal of frequency 4×107Hz . The apparent frequency of the signal produced by the rocket observed by the observer on earth will be
View SolutionA train is moving in the north-south direction with a speed of 108kmh−1. Find the e.m.f. generated between two wheels, if the length of the axle is 2m. Assume that the vertical component of earth's field is 8.0×10−5Wbm−2
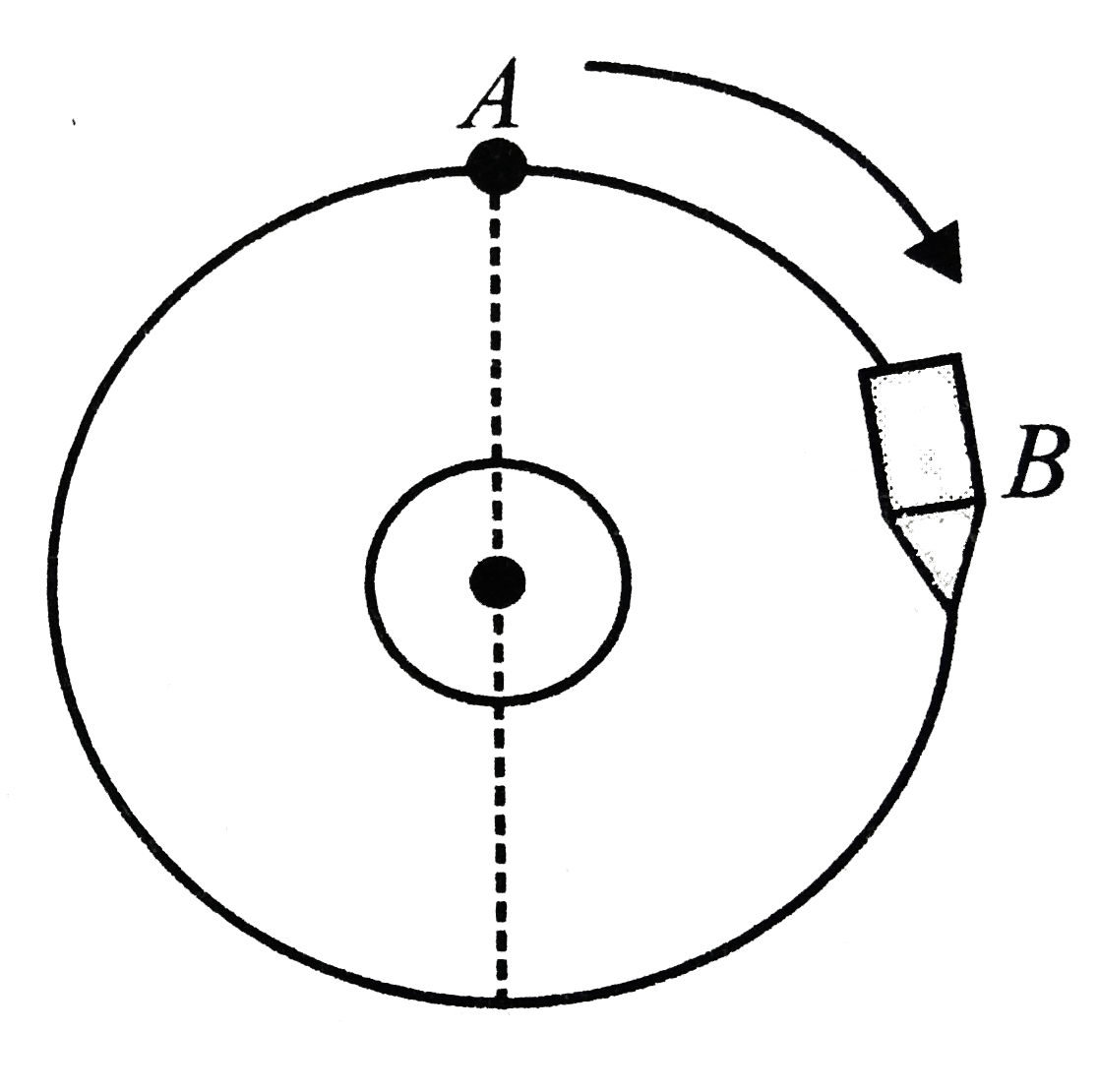
View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
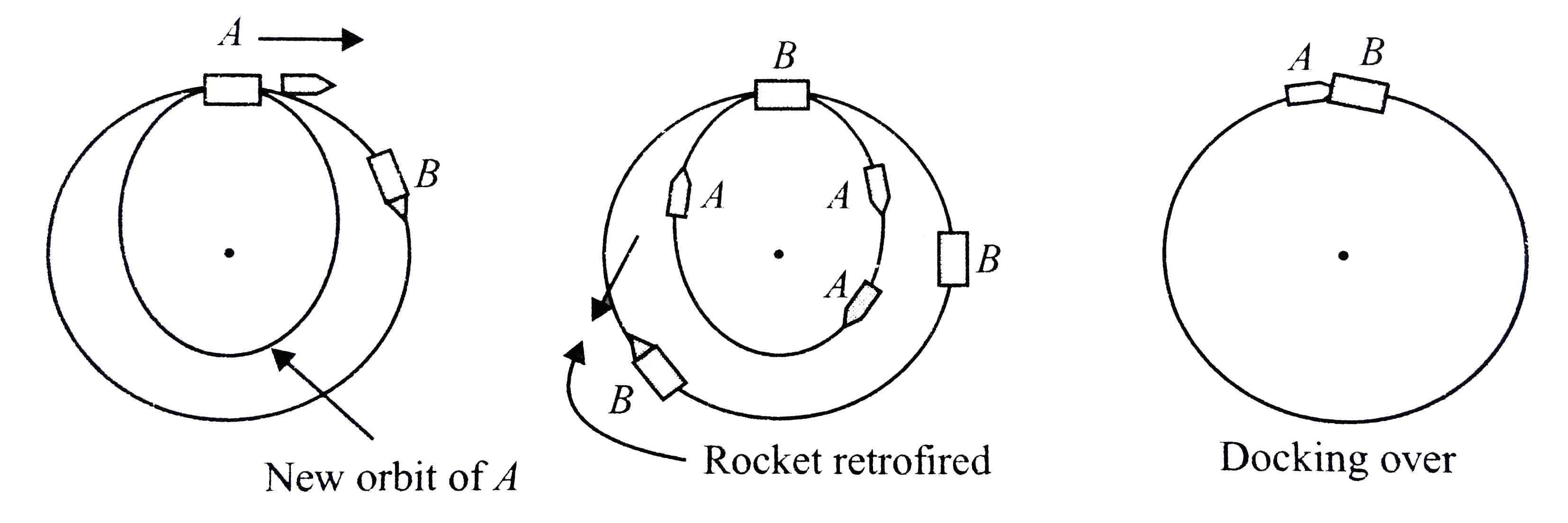
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions. After once returning to the original point, i.e., the place from where the rockets have been fired, in which direction and with what extent the rockets have to be fired from the satellite to again come back in the original orbit?View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
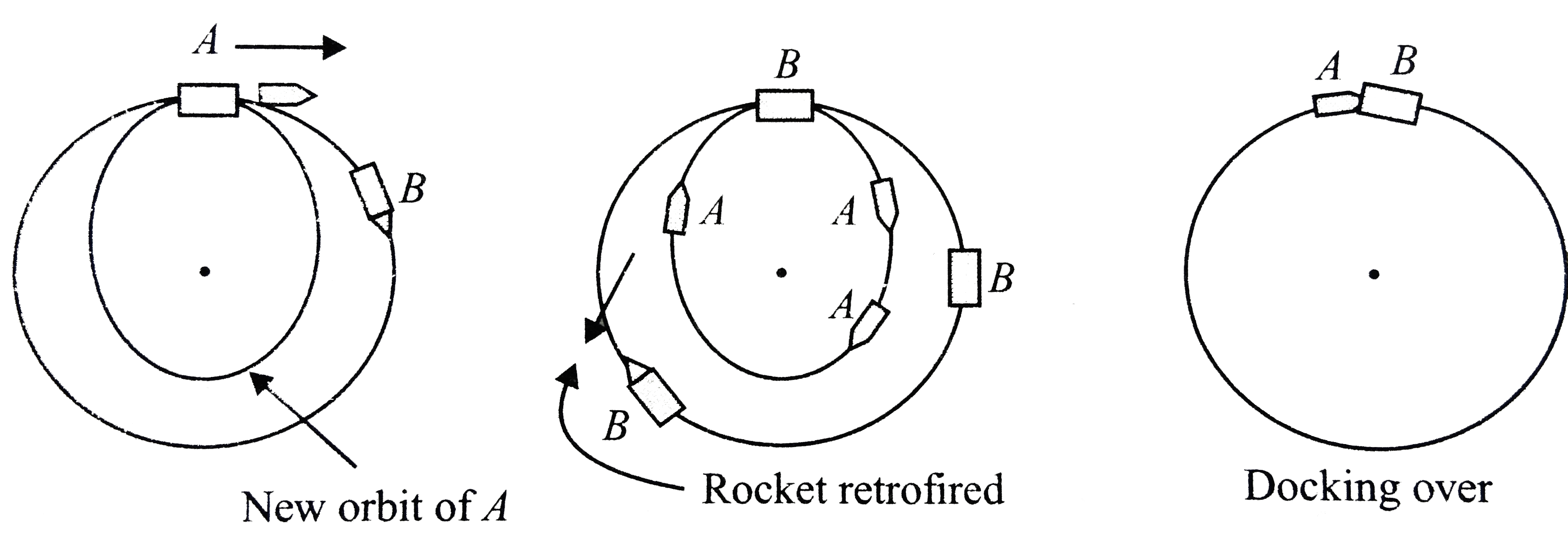
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions.
To dock A and B in the above-described situation, one can use the rocket system of either one, i.e., either of A or of B. To accomplish docking in the minimum possible time which is the best way?View SolutionAn unmanned satellite A and a spacecraft B are orbiting around the earth in the same circular orbit as shown.
 The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
The spacecraft is ahead of the satellite by some time. Let us consider that some technical problem has arisen in the satellite and the astronaut from B has made it correct. For this to be done docking of two (A and B) is required (in layman terms connecting A and B). To achieve this, the rockets of A have been fired in forward direction and docking takes place as shown in the figure below:
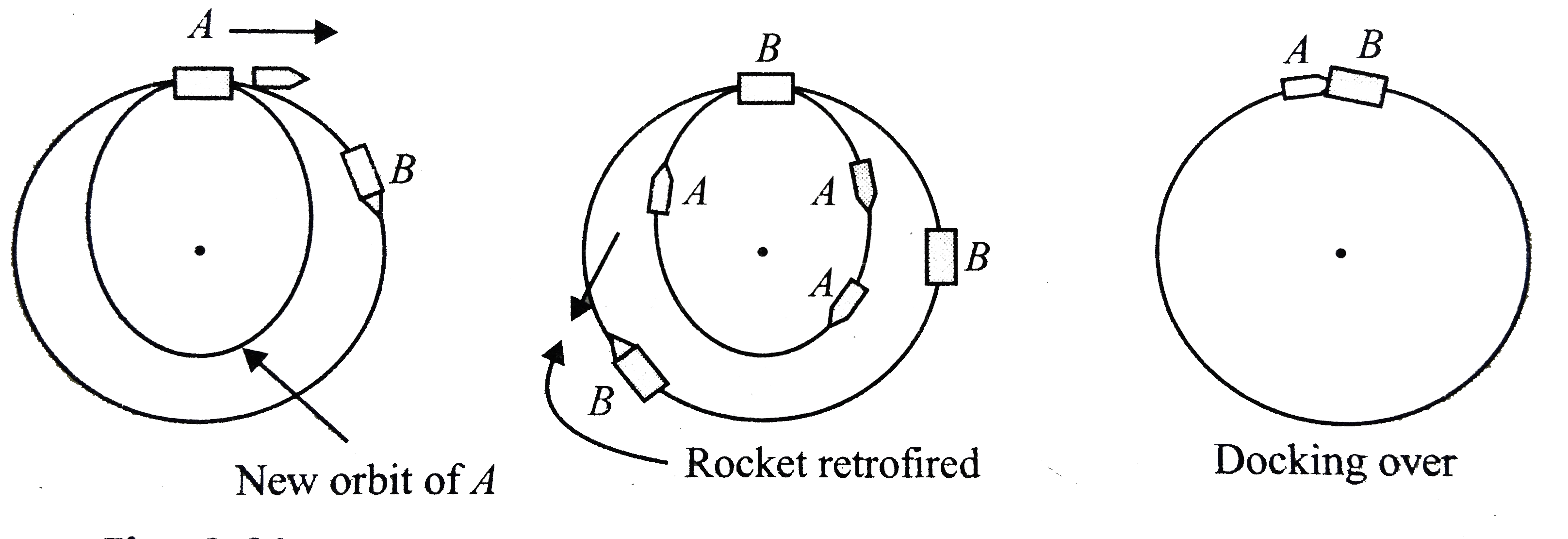
Take mass of the earth =5.98×1024kg
Radius of the earth =6400km
Orbital radius =9600km
Mass of satellite A=320kg
Mass of spacecraft =3200kg
Assume that initially spacecraft B leads satellite A by 100s, i.e., A arrives at any particle position after 100s of B’s arrival. Based on the above information answer the following questions
The initial total energy and time period of satellite are, respectively,View SolutionA rocket is fired vertically with a speed of 5kms−1 from the earth's surface. How far from the earth does the rocket go before returning to the erath? Mass of the earth =6.0×1024kg, mean radius of the earth =6.4×106m.G=6.67×10−11Nm2kg−2.
View SolutionA rocket is fired vertically with a speed of 5 kms−1 from the earth's surface. How far from the earth does the rocket go before returning to the earth ? Mass of earth=6.0×1024kg, mean radius of the earth =6.4×106m, G=6.67×10−11Nm2Kg−2.
View Solution

