A man piles 150 tookpicks in layers so that each layer has one less tookpick than the below. If the top layer has three tookpicks , how many layers are there ?
15
17
20
148
The correct Answer is:A
To solve the problem of how many layers of toothpicks are stacked, we can follow these steps:
Step 1: Understand the Problem
The problem states that a man piles 150 toothpicks in layers, with each layer having one less toothpick than the layer below it. The top layer has 3 toothpicks.
Step 2: Define the Variables
Let:
- n = number of layers
- The number of toothpicks in the top layer (1st layer) = 3
- The number of toothpicks in the 2nd layer = 4
- The number of toothpicks in the 3rd layer = 5
- Continuing this way, the number of toothpicks in the n-th layer = 3+(n−1)
Step 3: Write the Sum of the Toothpicks
The total number of toothpicks in n layers can be expressed as:
Total Toothpicks=3+4+5+…+(3+(n−1))
This can be rewritten as:
Total Toothpicks=n−1∑k=0(3+k)=3n+n−1∑k=0k
Using the formula for the sum of the first n−1 integers, n−1∑k=0k=(n−1)n2, we can substitute:
Total Toothpicks=3n+(n−1)n2
Step 4: Set Up the Equation
We know the total number of toothpicks is 150:
3n+(n−1)n2=150
Step 5: Clear the Fraction
To eliminate the fraction, multiply the entire equation by 2:
2(3n)+(n−1)n=300
This simplifies to:
6n+n2−n=300
or:
n2+5n−300=0
Step 6: Factor the Quadratic Equation
Now we need to factor the quadratic equation n2+5n−300=0. We look for two numbers that multiply to -300 and add to 5. These numbers are 20 and -15:
(n+20)(n−15)=0
Step 7: Solve for n
Setting each factor to zero gives:
1. n+20=0 → n=−20 (not valid since n must be positive)
2. n−15=0 → n=15
Conclusion
Thus, the number of layers is n=15.
The problem states that a man piles 150 toothpicks in layers, with each layer having one less toothpick than the layer below it. The top layer has 3 toothpicks.
Let:
- n = number of layers
- The number of toothpicks in the top layer (1st layer) = 3
- The number of toothpicks in the 2nd layer = 4
- The number of toothpicks in the 3rd layer = 5
- Continuing this way, the number of toothpicks in the n-th layer = 3+(n−1)
The total number of toothpicks in n layers can be expressed as:
Total Toothpicks=3+4+5+…+(3+(n−1))
This can be rewritten as:
Total Toothpicks=n−1∑k=0(3+k)=3n+n−1∑k=0k
Using the formula for the sum of the first n−1 integers, n−1∑k=0k=(n−1)n2, we can substitute:
Total Toothpicks=3n+(n−1)n2
We know the total number of toothpicks is 150:
3n+(n−1)n2=150
To eliminate the fraction, multiply the entire equation by 2:
2(3n)+(n−1)n=300
This simplifies to:
6n+n2−n=300
or:
n2+5n−300=0
Now we need to factor the quadratic equation n2+5n−300=0. We look for two numbers that multiply to -300 and add to 5. These numbers are 20 and -15:
(n+20)(n−15)=0
Setting each factor to zero gives:
1. n+20=0 → n=−20 (not valid since n must be positive)
2. n−15=0 → n=15
Thus, the number of layers is n=15.
Topper's Solved these Questions
Similar Questions
Which layer has more cellulose ?
View SolutionHow many layers form the diffusion membrane ?
View SolutionWhich of these has a layered arrangement?
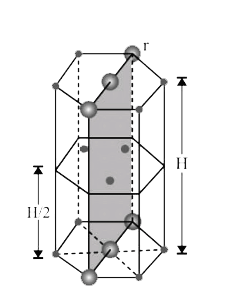
View SolutionIn a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The empty space in this hcp unit cell is
(a)74%
(b)48.6%
(c)32%
(d)26%
View SolutionIn a hexagonal system system of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-packed is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed overt the first layer so that they touch each other and represent the second layer so that they touch each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is converted with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
(a)4
(b)6
(c)12
(d)17
View SolutionIn a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be r.
The number of atom in this hcp unit cell is
View SolutionHow many germ layers are present in the embryonic stage of platyhelminthes?
View SolutionName the innermost layer of cortex that has barrel shaped cells.
View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The volume of this HCP unit cell is

View SolutionIn hexagonal systems of crystals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are regular hexagons and three atoms are sandwiched in between them. A space-filling model of this structure, called hexagonal close-packed (HCP), is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spheres are then placed over the first layer so that they touch each other and represent the second layer. Each one of these three spheres touches three spheres of the bottom layer. Finally, the second layer is covered with a third layer that is identical to the bottom layer in relative position. Assume radius of every sphere to be ‘r’.
The empty space in this HCP unit cell is :
View Solution
