Question

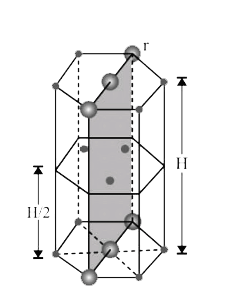
In a hexaonal system system of cycstals, a frequently encountered arrangement of atoms is described as a hexagonal prism. Here, the top and bottom of the cell are refular hexagons, and three atoms are sandwiched in between them. A space-cilling model of this structure, called hexagonal close-paked is constituted of a sphere on a flat surface surrounded in the same plane by six identical spheres as closely as possible. Three spherres are then placed overt the first layer so that they toych each other and represent the second layer so that they toych each other and present the second layer. Each one of the three spheres touches three spheres of the bottom layer. Finally, the second layer is convered with a third layer identical to the bottom layer in relative position. Assume the radius of every sphere to be ${\displaystyle r}$.
The empty space in this hcp unit cell is

(a)${\displaystyle 74\%}$

(b)${\displaystyle 48.6\%}$

(c)${\displaystyle 32\%}$

(d)${\displaystyle 26\%}$

Options

A. `74%`
B. `48.6%`
C. `32%`
D. `26%`

Answer

D

Explanation

To find the empty space in a hexagonal close-packed (hcp) unit cell, we need to calculate the packing efficiency and then determine the empty space based on that efficiency. Here’s a step-by-step solution:

Step 1: Understand the structure
In a hexagonal close-packed structure, we have:
- Two hexagonal faces (top and bottom) with regular hexagons.
- Three layers of atoms: the first layer (A), the second layer (B), and the third layer (A again).

Step 2: Determine the number of atoms in the unit cell
In the hcp structure:
- Each hexagonal face contributes 6 atoms (corners) and 3 atoms in the middle layer.
- The effective number of atoms (Z) in one unit cell is 6.

Step 3: Calculate the volume of atoms in the unit cell
The volume of one atom (considered as a sphere) is given by the formula:
\( \text{Volume of one sphere} = \frac{4}{3} \pi r^3 \)
Thus, the total volume of atoms in the unit cell is:
\( \text{Total volume of atoms} = Z \times \text{Volume of one sphere} = 6 \times \frac{4}{3} \pi r^3 = 8 \pi r^3 \)

Step 4: Calculate the volume of the unit cell
The edge length (a) of the hexagonal unit cell can be expressed in terms of the radius (r) of the spheres. For hcp, the relationship is:
\( a = 2r \)
The volume of the hexagonal prism (unit cell) can be calculated using the formula for the volume of a hexagonal prism:
\( \text{Volume of unit cell} = \frac{3\sqrt{3}}{2} a^2 c \)
Where \(c\) is the height of the unit cell. In hcp, the height \(c\) can be approximated as \( \frac{4r}{\sqrt{2}} \) (considering the arrangement of the spheres).

Step 5: Substitute the values
Substituting \(a = 2r\) into the volume of the unit cell:
\( \text{Volume of unit cell} = \frac{3\sqrt{3}}{2} (2r)^2 \left(\frac{4r}{\sqrt{2}}\right) \)
Calculating this gives:
\( = \frac{3\sqrt{3}}{2} \times 4r^2 \times \frac{4r}{\sqrt{2}} = 12\sqrt{3}r^3 \)

Step 6: Calculate packing efficiency
The packing efficiency (PE) can be calculated using the formula:
\( \text{Packing Efficiency} = \frac{\text{Volume of atoms in unit cell}}{\text{Volume of unit cell}} \times 100 \)
Substituting the values:
\( \text{Packing Efficiency} = \frac{8\pi r^3}{12\sqrt{3}r^3} \times 100 \)
This simplifies to:
\( = \frac{8\pi}{12\sqrt{3}} \times 100 \)
Calculating this gives approximately 74%.

Step 7: Calculate empty space
To find the empty space in the unit cell, we subtract the packing efficiency from 100%:
\( \text{Empty Space} = 100\% - \text{Packing Efficiency} = 100\% - 74\% = 26\% \)

Final Answer
Thus, the empty space in the hcp unit cell is 26%.

---