Draw any triangle ABC . Bisect side AB at D . Through D , draw a line parallel to BC , meeting AC in E . Measure AE and EC .
Step by step video & image solution for Draw any triangle A B C . Bisect side A B at D . Through D , draw a line parallel to B C , meeting A C in E . Measure A E and E C . by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Topper's Solved these Questions
Similar Questions
Draw any triangle ABC . Bisect side AB at D . Through D , draw a line parallel to BC , meeting AC in E . Measure AE and EC .
View SolutionInternal bisector of ∠A of triangle ABC meets side BC at D. A line drawn through D perpendicular to AD intersects the side AC at E and the side AB at F. If a, b, c represent sides of ΔABC, then
View SolutionP is any point on base BC of ABC and D is the mid-point of BC.DE is drawn parallel to PA to meet AC at E. If ar(ABC)=12cm2 , then find area of EQC
View SolutionFill the blanks in the following so that each of the following statements is true.
(i) Sides opposite to equal angles of a triangle are ......
(ii) Angle opposite to equal sides of a triangle are .....
(iii) In an equilateral triangle all angles are .....
(iv) In a ΔABC if ∠A = ∠C , then AB = ......
(v) If altitudes CE and BF of a triangle ABC are equal, then AB = ....
(vi) In an isosceles triangle ABC with AB = AC, if BD and CE are its altitudes, then BD is …… CE.
(vii) In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……View SolutionTriangles on the same base and between the same parallels are equal in area. GIVEN : Two triangles ABC and PBC on the same base BC and between the same parallel lines BC and AP. TO PROVE : ar(ABC)=ar(PBC) CONSTRUCTION : Through B, draw BDCA intersecting PA produced in D and through C, draw CQBP, intersecting line AP in Q.
View SolutionIf triangle ABC is similar to triangle DEF such that BC=3CM,EF=4cm and area of triangle ABC=54cm2 . Determine the area of triangle DEF.
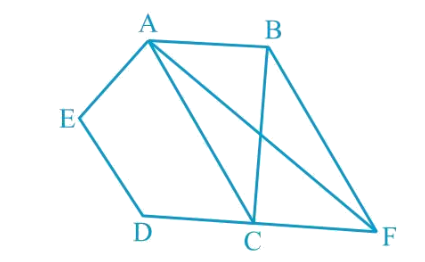
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
 View Solution
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)
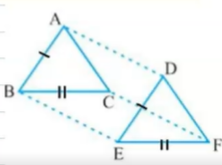
View SolutionIf ABC and DEF are two triangles such that AB, BC are respectively equal and parallel to DE, EF, then show that Quadrilateral ABED is a parallelogram Quadrilateral BCFE is a parallelogram AC=DF (iv) ABC ≅ DEF
 View Solution
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View Solution

