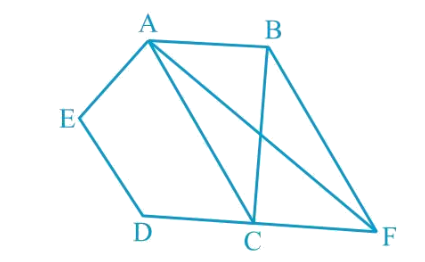
In Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that ar(ACB)=ar(ACF) (ii) ar(AEDF)=ar(ABCDE)

(i)A pentagon ABCDE, BF is parallel to AC
To Prove: Ar(ACB)=Ar(ACF)
Ar(AEDF)=Ar(ABCDE)
△ACBand△ACF lies on same base AC and are between same parallel AC and BF
∴Ar(△ACB)=Ar(△ACF)→eq(1)
(ii) add Ar(AEDC) both sides
Ar(△ACB)+Ar(AEDC)=Ar(△ACF)+Ar(AEDC)
Ar(ABCDE)=Ar(AEDF)
Topper's Solved these Questions
Similar Questions
In Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionABCD is a trapezium with AB∣∣DC . A line parallel to AC intersects AB at X and BC at Y. Prove that ar(ADX)=ar(ACY).
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD . Show that ar(APB)+ar(PCD)=12ar(^(gm)ABCD) aR(APD)+ar(PBC)=ar(APB)+ar(PCD)
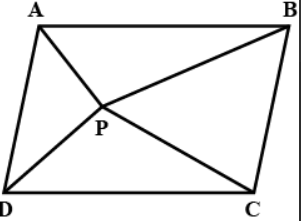
View SolutionIn Figure, P is a point in the interior of a parallelogram ABCD. Show that ar(APB)+ar(PCD)=12ar (||gmABCD) ar (APD)+ar (PBC)=ar (APB)+ar(PCD)

View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
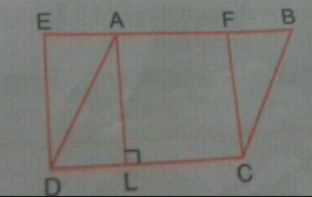
View SolutionIn Figure, ABCD is a parallelogram and EFCD is a rectangle. Also AL⊥DC. Prove that : ar(ABCD)=ar(EFCD) ar(ABCD)=DC×AL

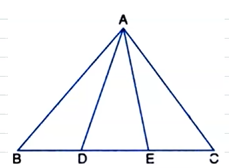
View SolutionIn Figure DandE are two points on BC such that BD=DE=EC Show that ar(ABD)=ar(ADE)=ar(AEC)
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
View Solution
