A field in the form of a parallelogram has one of its diagonals 42 m long the perpendicular distance of this diagonal from either of the outlying vertices is 10.8 m. Find the area of the field.
To find the area of the field in the form of a parallelogram with the given dimensions, we can follow these steps:
1. Identify the given values:
- Length of the diagonal (d) = 42 m
- Perpendicular distance from the diagonal to either of the outlying vertices (h) = 10.8 m
2. Understand the relationship between the area of the parallelogram and the triangles formed by the diagonal:
- The diagonal of the parallelogram divides it into two triangles (let's call them T1 and T2).
- The area of the parallelogram can be calculated as the sum of the areas of these two triangles.
3. Calculate the area of one triangle (T1):
- The area of a triangle is given by the formula:
Area=12×base×height
- Here, the base is the length of the diagonal (42 m) and the height is the perpendicular distance (10.8 m).
- Therefore,
Area of T1=12×42×10.8
4. Perform the calculation for T1:
- Calculate the area:
Area of T1=12×42×10.8=21×10.8=226.8m2
5. Calculate the total area of the parallelogram:
- Since the area of T2 is equal to the area of T1, the total area of the parallelogram (A) is:
A=Area of T1+Area of T2=226.8+226.8=2×226.8
- Thus,
A=453.6m2
Final Answer:
The area of the field is 453.6 m².
- Length of the diagonal (d) = 42 m
- Perpendicular distance from the diagonal to either of the outlying vertices (h) = 10.8 m
- The diagonal of the parallelogram divides it into two triangles (let's call them T1 and T2).
- The area of the parallelogram can be calculated as the sum of the areas of these two triangles.
- The area of a triangle is given by the formula:
Area=12×base×height
- Here, the base is the length of the diagonal (42 m) and the height is the perpendicular distance (10.8 m).
- Therefore,
Area of T1=12×42×10.8
- Calculate the area:
Area of T1=12×42×10.8=21×10.8=226.8m2
- Since the area of T2 is equal to the area of T1, the total area of the parallelogram (A) is:
A=Area of T1+Area of T2=226.8+226.8=2×226.8
- Thus,
A=453.6m2
The area of the field is 453.6 m².
Topper's Solved these Questions
Similar Questions
A field in the form of a parallelogram has one of its diagonals 42 m long the perpendicular distance of this diagonal from either of the outlying vertices is 10.8 m. Find the area of the field.
View SolutionOne diagonal of a parallelogram is 70 cm and the perpendicular distance of this diagonal from either of the outlying vertices is 27 cm. The area of the parallelogram (in sq. cm) is (a) 1800 (b) 1836 (c) 1890 (d) 1980
View Solution
Knowledge Check
One diagonal of a parallelogram is 40 cm and the perpendicular distance of this diagonal from either of the outlying vertices is 19 cm. The area of the parallelogram (in sq cm) is
A700 cm2B380 cm2C760 cm2D1140 cm2A parallelogram has sides 30 cm and 20 cm and one of its diagonal is 40 cm long. Then its area is :
A75√5cm2B245cm2C150√15cm2D300cm2A parallelogram has sides 30 m, 70 m and one of its diagonals is 80 m long. Its area will be
A600 m2B1200√3m2C1200 m2D600√3m2
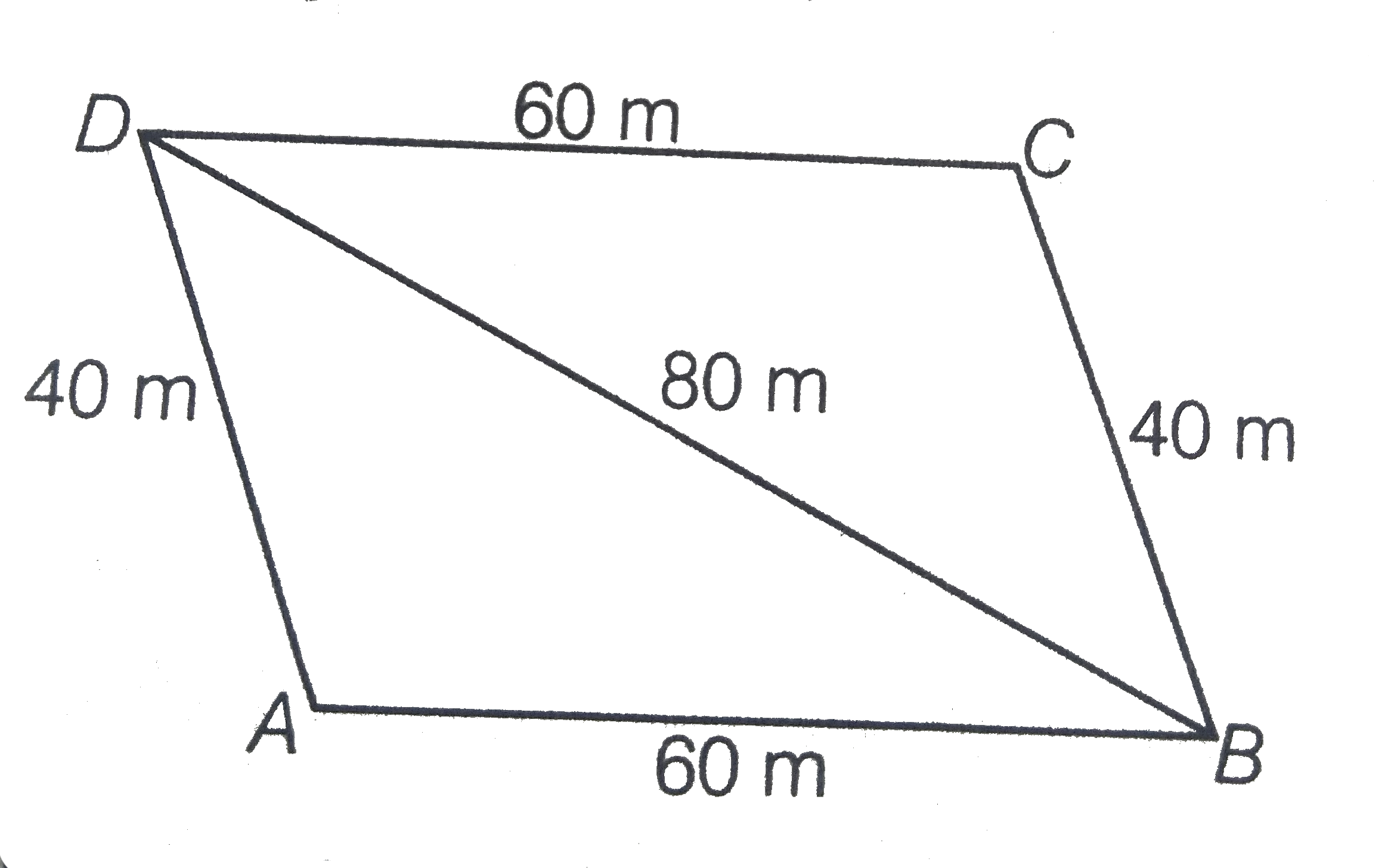
A field in the form of a parallelogram has sides 60 m and 40 m and one of its diagonals is 80 m long. Find the area of the parallelogram.
View Solution30. In a parallelogram ABCD, the diagonal AC measures 34m and the perpendicular distanceof AC from either of the vertices B and D is 12m. The area of the parallelogram isa
View SolutionThe area of a quadrilateral is 360m2 and the perpendiculars drawn to one of the diagonal from the opposite vertices are 10m and 8m. Find the length of the diagonal.
View SolutionA diagonal of a quadrilateral is 30.5m long. The perpendiculars to the diagonal from the opposite vertices are of lengths 8.5m and 7.5m.Find the area of the quadrilateral
View SolutionOne diagonal of a quadrilateral is 20 m long and the perpendiculars to it from the opposite vertices are 8.5 m and 11 m. Find the areaof the quadrilateral.
View Solution
