Two towns A and B are situated on the same side of a straight road at distances a and brespectively perpendiculars drawn from A and B meet the road at point C and D respectively.The distance between C and D is c. A hospital is to be built at a point P on the road such thatthe distance APB is minimum. Find position of P.
Step by step video & image solution for Two towns A and B are situated on the same side of a straight road at distances a and brespectively perpendiculars drawn from A and B meet the road at point C and D respectively.The distance between C and D is c. A hospital is to be built at a point P on the road such thatthe distance APB is minimum. Find position of P. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Two trees A and B are on the same side of a river. From a point C in the river, the river, the distance of trees A and B are 250 m and 300 m and respectively. If angle of C=45^0. find the distance between trees.
View SolutionIn a class room 4 friends are seated at the point A,B,C,D as shown in figure.
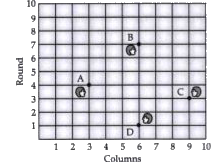
Find the distance between B and C.
View Solution
Knowledge Check
If A, B and C are three points position vectors a, b and c respectively, then perpendicular distance of A from the line joining B and C is
A|a×b×c|2(b×c)B|a×b+b×c+c×a|2|(b−c)|C|a×b+b×c+c×a||(b−c)|DNone of these.Two men A and B cover the distance of 21 km from P to Q at a speed of 3 km/h and 4 km/h respectively. When B reaches at point Q, he returns and meets at point C to A. Find the distance of C from P.
A15B10C18D20
Two runners Shiva and Abhishek start running to and fro between opposite ends A and B of a straight road towards each other from A and B respectively. They meet first time at a point 0.75D from A, where D is the distance between A and B. Find the point of their 6th meeting.
View SolutionTwo triangle ABC and DBC lie on the same side of the base BC . From a point P on BC, PQ||AB and PR||BD are drawn. They meet AC in Q and DC in R respectively. Prove that QR||AD.
View SolutionThe distance between the middle point of BC and the foot of the perpendicular from A is:
View SolutionThe distance between the middle point of BC and the foot of the perpendicular from A is:
View SolutionLet AB and CD are two parallel chords of circle whose radius is 5 units. If P and Q are mid points of AB and CD respectively such that PA.PB=9,QC.QD=16, then distance betweẹn AB and CD is
View SolutionTwo triangle ABC and DBC lie on the same side of the base BC . From a point P on BC,PQAB AND PRBD ARE DRAWN. They meet AC in Q and DC in R respectively. Prove that QRAD.
View Solution
