In Figure, PQRS is a square. Determine ∠SRP.
PQRS is a square
PS =PR and
∠ PSR=90°,
In△PSR
PS=PR
∠1=∠2 (Angles opposite to equal sides are equal )
∠1+∠2+∠PSR=180°
2×∠1+90°=180°
∠1=45°
angleSRP=45°
Topper's Solved these Questions
Similar Questions
If PQRS is a square, then write the measure of ∠SRP
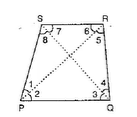
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
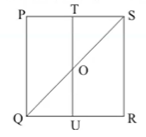
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View SolutionIn Fig. 15.77, PQRS is a square of side 4 cm. Find the area of the shaded region. (FIGURE)
View SolutionIn Figure, PQR is a triangle and S is any point in its interior, show that SQ+SR<PQ+PR Given : S is any point in the interior of PQR To Prove : SQ+SR<PQ+PR Construction: Produce QS to meet PR in T
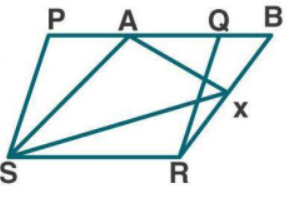
View SolutionIn Figure, PQRS and ABRS are parallelograms and X is any point on side BR. Show that : ar(^(gm)PQRS)=ar(^(gm)ABRS) ar(AXS)=12ar(PQRS)
View SolutionPQRSTU is a regular hexagon. Determine each angle of PQT .
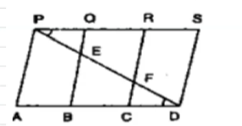
View SolutionIn Figure, PSDA is a parallelogram in which PQ=QR=RS and APBQCR. Prove that ar ( PQE)= ar ( CFD).
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
View Solution