Construct a quadrilateral in which AB=5.4cm, BC=2.5cm, CD=4cm, AC=6.5cm and BD=5cm.
To construct the quadrilateral ABCD with the given dimensions, follow these steps:
Step-by-Step Construction:
1. Draw Line Segment AB:
- Use a ruler to draw a line segment AB measuring 5.4 cm.
2. Construct Circle with Center B:
- Using a compass, place the pointer on point B and draw a circle with a radius of 2.5 cm (this represents BC).
3. Construct Circle with Center A:
- Without changing the compass width, place the pointer on point A and draw another circle with a radius of 6.5 cm (this represents AC).
4. Locate Point C:
- The intersection of the two circles you just drew will give you point C. Mark this intersection as point C.
5. Draw Line Segment CD:
- From point C, use a ruler to measure and draw a line segment CD that is 4 cm long.
6. Construct Circle with Center D:
- Now, using a compass, place the pointer on point C and draw a circle with a radius of 4 cm (this represents CD).
7. Construct Circle with Center B:
- Next, using a compass, place the pointer on point B and draw a circle with a radius of 5 cm (this represents BD).
8. Locate Point D:
- The intersection of the two circles you just drew will give you point D. Mark this intersection as point D.
9. Complete the Quadrilateral:
- Finally, connect points A, B, C, and D in order to complete the quadrilateral ABCD.
- Use a ruler to draw a line segment AB measuring 5.4 cm.
- Using a compass, place the pointer on point B and draw a circle with a radius of 2.5 cm (this represents BC).
- Without changing the compass width, place the pointer on point A and draw another circle with a radius of 6.5 cm (this represents AC).
- The intersection of the two circles you just drew will give you point C. Mark this intersection as point C.
- From point C, use a ruler to measure and draw a line segment CD that is 4 cm long.
- Now, using a compass, place the pointer on point C and draw a circle with a radius of 4 cm (this represents CD).
- Next, using a compass, place the pointer on point B and draw a circle with a radius of 5 cm (this represents BD).
- The intersection of the two circles you just drew will give you point D. Mark this intersection as point D.
- Finally, connect points A, B, C, and D in order to complete the quadrilateral ABCD.
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
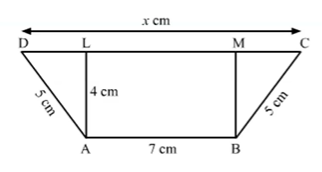
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
View SolutionIn a ABC, D and E are points on the sides AB and AC respectively. For each of the following cases show that DEBC : AB=10.8cm, BD=4.5 cm, AC=4.8cm and AE=2.8cm (ii) AD=5.7cm, BD=9.5cm, AE=3.3cm and EC=5.5cm .
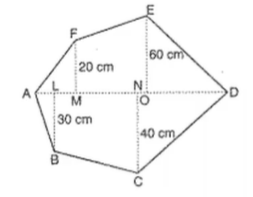
View SolutionFind the area of the following polygon, if AL=10cm, AM=20cm, AN=50cm, AO=60cm and AD=90cm.
View SolutionIn Fig. 10.57, a circle is inscribed in a quadrilateral ABCD in which ∠B=90o . If AD=23cm , AB=29cm and DS=5cm , find the radius r of the circle. (FIGURE)
View SolutionWhich of the following pairs of triangles are congruent? If they are congruent, write out the pairs of equal angles. ABC:AB=3cm, BC=4cm, CA=2 cm DEF:DE=2 cm, EF=3 cm and FD=4 cm PQR:PQ=17 cm, QR=15 cm, PR=18 cm DEF:DE=18 cm, EF=17 cm, DF=15 cm .
View SolutionIn which of the following cases can a right triangle ABC be constructed? AB=5 cm, BC=7 cm, AC=10 cm AB=7 cm, BC=8 cm, AC=12 cm AB=8 cm, BC=17 cm, AC=15 cm None of these
View SolutionIn a ABC , D and E are points on AB and AC respectively such that DE/BC . If AD=2.4cm, AE=3.2cm, DE=2cm and BC=5cm , find BD and CE .
View SolutionIn Figure, ABCD is a parallelogram. If AB=12cm,AE=7.5cm,CF=15cm, then AD=

(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 10.5 cm
View SolutionIn Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=5cm, AC=10cm, BD=1.5cm and CD=3.5cm (ii) AB=4cm, AC=6cm, BD=1.6cm and CD=2.4cm (iii) AB=8cm, AC=24cm, BD=6cm and BC=24cm
View Solution
