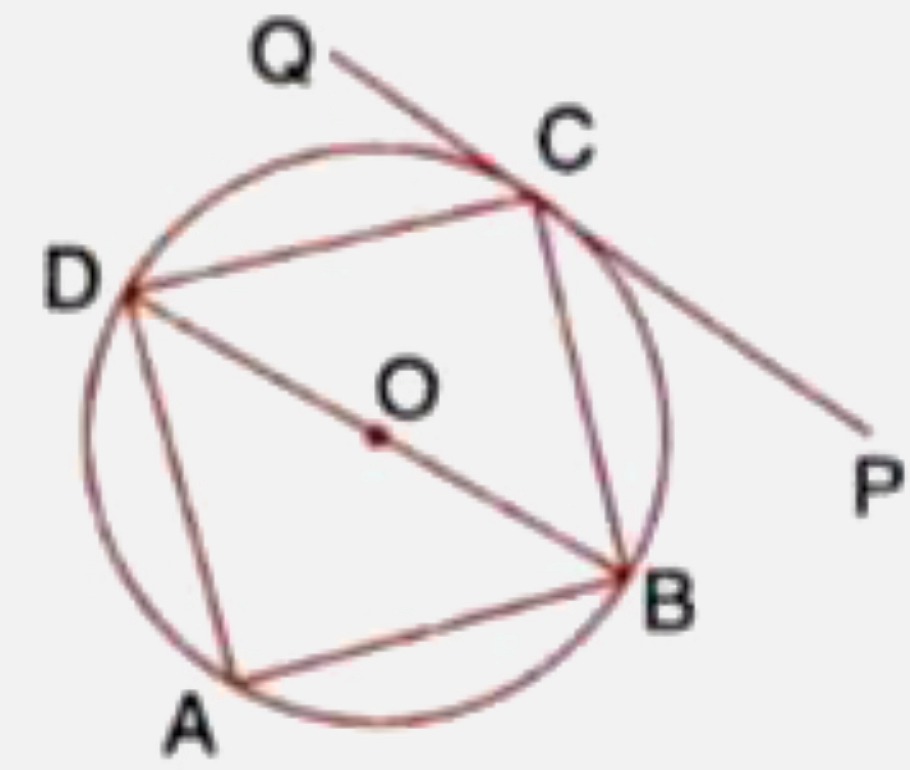
ABCD is a cyclic quadrilateral and PQ is a tangent to the circle at C. If BD is a diameter, measure of (i) LDBC (ii) LBCP (iii) LBDC (iv) LADB
∠DAB=90∘
in ∠ABD
∠A+∠B+∠D=180∘
90∘+60∘+∠D=180∘
∠ADB=180∘−150∘=30∘
∠ADB=30∘
∠BDC=∠DCQ
∠DBC=40∘
∠DCB=90∘
∠DCQ+∠DCB+∠BCP=180∘
40∘+90∘+∠BCP=180∘
∠BCP=180∘−130∘=50∘
∠BCP=50∘
∠BDC=∠BCP(alternate segment theorem)
∠BDC=50∘
Answer
Similar Questions
In the given figure, ABCD is a cyclicquadrilateral, PQ is tangent to the circle at point C and BD is its diameter.
If ∠DCQ=40∘ and ∠ABD=60∘ find
(i) ∠DBC
(ii) ∠BCP
(iii) ∠ADB
View SolutionIn Figure, ABCD is a cyclic quadrilateral; O is the centre of the circle. If ∠BOD=1600, find the measure of ∠BPD
View Solution
Knowledge Check
ABCD is a cyclic quadrilateral PQ is a tangent at B. If ∠DBQ=65∘, then ∠BCD is:
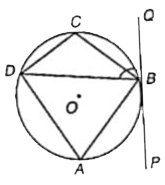 A35∘B85∘C115∘D90∘
A35∘B85∘C115∘D90∘ABCD is a cyclic quadrilateral. PBQ is a tangent drawn from the point B of the circle, if ∠DBP=65∘, then measures of ∠BCD is
A65∘B90∘C110∘D115∘ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠CAB=48∘, then what is the value (in degrees) of ∠ADC?
A52B77C138D142
In the figure ABCD is a cyclic quadrilateral with BC=CD. TC is tangent to the circle at point C and DC is produced to point G. If ∠BCG=108∘ and O is the centre of the circle find
(i) angle BCT
(ii) angle DOC

View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
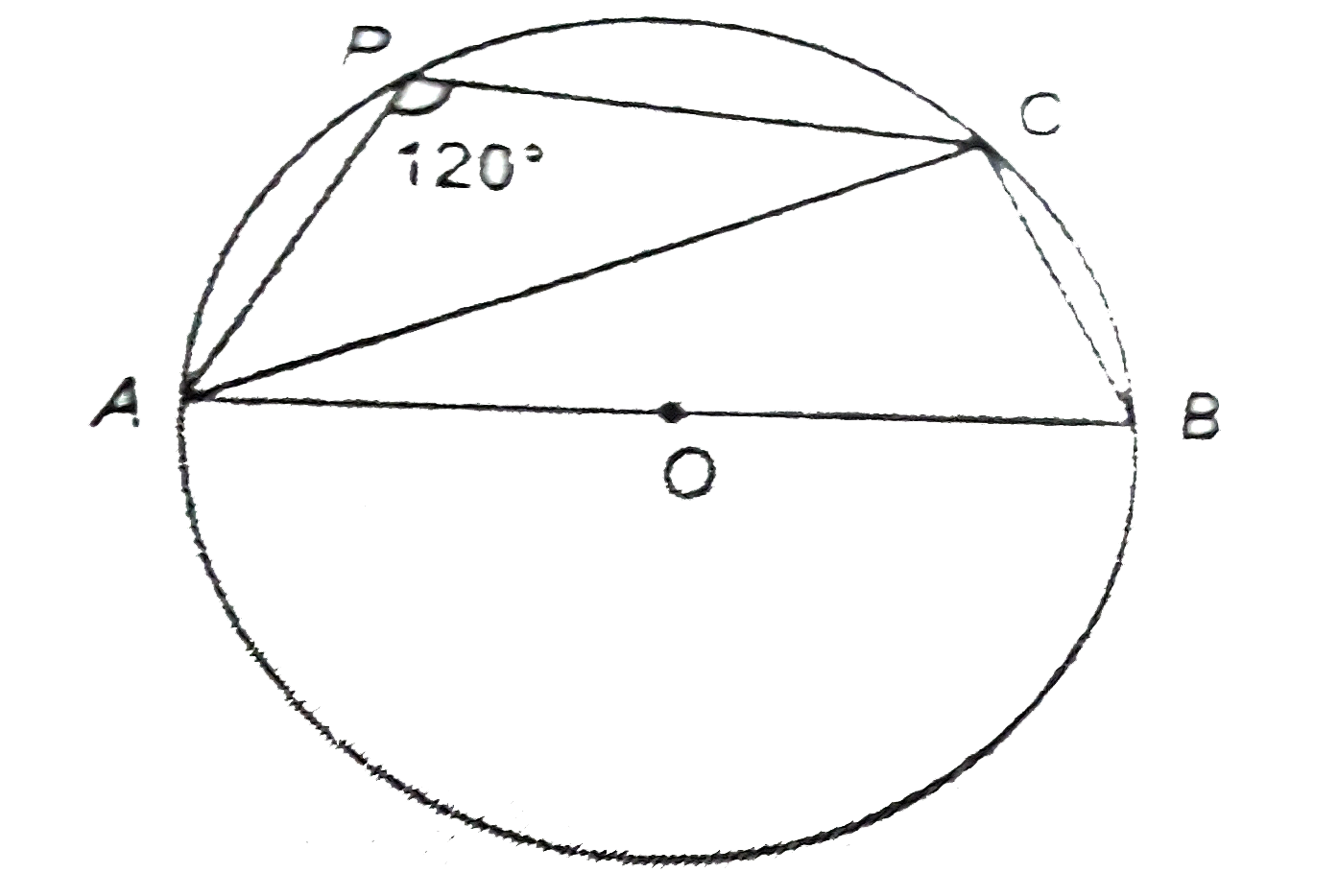
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.

View SolutionIn a cyclic quadrilateral ABCD, diagonal AC bisects ∠C. Prove that the tangent to thecircle at A is parallel to the diagonal BD.
View SolutionABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If ∠ADC=130∘, find ∠BAC.

View Solution