In a cyclic quadrilateral ABCD, diagonal AC bisects /C. Prove that th

The diagonals AC and BD of a cyclic quadrilateral ABCD intersect each other at the point P. Then,it is always true that
AAP. CP = BP. DP
BAP.BP = CP. DP
CAP. CD = AB. CP
DBP. AB = CD.CP
The diagonals AC and BD of a cyclic quadrilateral ABCD inter sect each other at the point P. Then, it is always true that
A(a) $B P . A B = C D . C P$
B(b) $A P . C P = B P . D P$
C(c) $A P . B P = C P . D P$
D(d) $A P . C D = A B . C P$
In the given figure, ABCD is a cyclic quadrilateral and diagonals D bisect each other at P. If $∠ D B C = 60^{\circ} and ∠ B A C = 30^{\circ}$ , then $∠ B C D$ is:

A $90^{\circ}$
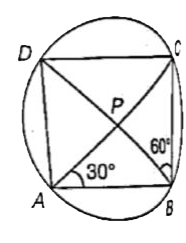B $60^{\circ}$
C $80^{\circ}$
Dnone of the above

In a cyclic quadrilateral ABCD, diagonal AC bisects $∠ C$ . Prove that the tangent to thecircle at A is parallel to the diagonal BD.