If P=2(L+M), what is W in terms of P and L?
P−2L
P−2L2
2L−P2
12(P−L)
The correct Answer is:B
To solve the equation P=2(L+M) for M in terms of P and L, we can follow these steps:
Step 1: Start with the given equation
We have the equation:
P=2(L+M)
Step 2: Divide both sides by 2
To isolate the term (L+M), we divide both sides of the equation by 2:
P2=L+M
Step 3: Subtract L from both sides
Next, we want to isolate M. We do this by subtracting L from both sides:
P2−L=M
Step 4: Rearranging the equation
We can rearrange this to express M clearly:
M=P2−L
Step 5: Final expression for M
This is our final expression for M in terms of P and L:
M=P−2L2
We have the equation:
P=2(L+M)
To isolate the term (L+M), we divide both sides of the equation by 2:
P2=L+M
Next, we want to isolate M. We do this by subtracting L from both sides:
P2−L=M
We can rearrange this to express M clearly:
M=P2−L
This is our final expression for M in terms of P and L:
M=P−2L2
Topper's Solved these Questions
Similar Questions
Knowledge Check
A rectangle has area A, length l, and width w. Which of the following represents w in terms of A and l?
Aw=A2lBw=AlCw=2AlDw=√Al
If the first, fifth and last terms of an A.P. is l, m, p, respectively, and sum of the A.P. is (l+p)(4p+m−5l)k(m−l) then k is
View SolutionThe first and last term of an A.P. are a and l respectively. If S is the sum of all the terms of the A.P. and the common difference is given by l2−a2k−(l+a) , then k= (a)S(b) 2S (c) 3S (d) none of these
View SolutionThe first and last term of an A.P. are a and l respectively. If S is the sum of all the terms of the A.P. and the common difference is given by l2−a2k−(l+a) , then k= (a)S(b) 2S (c) 3S (d) none of these
View Solution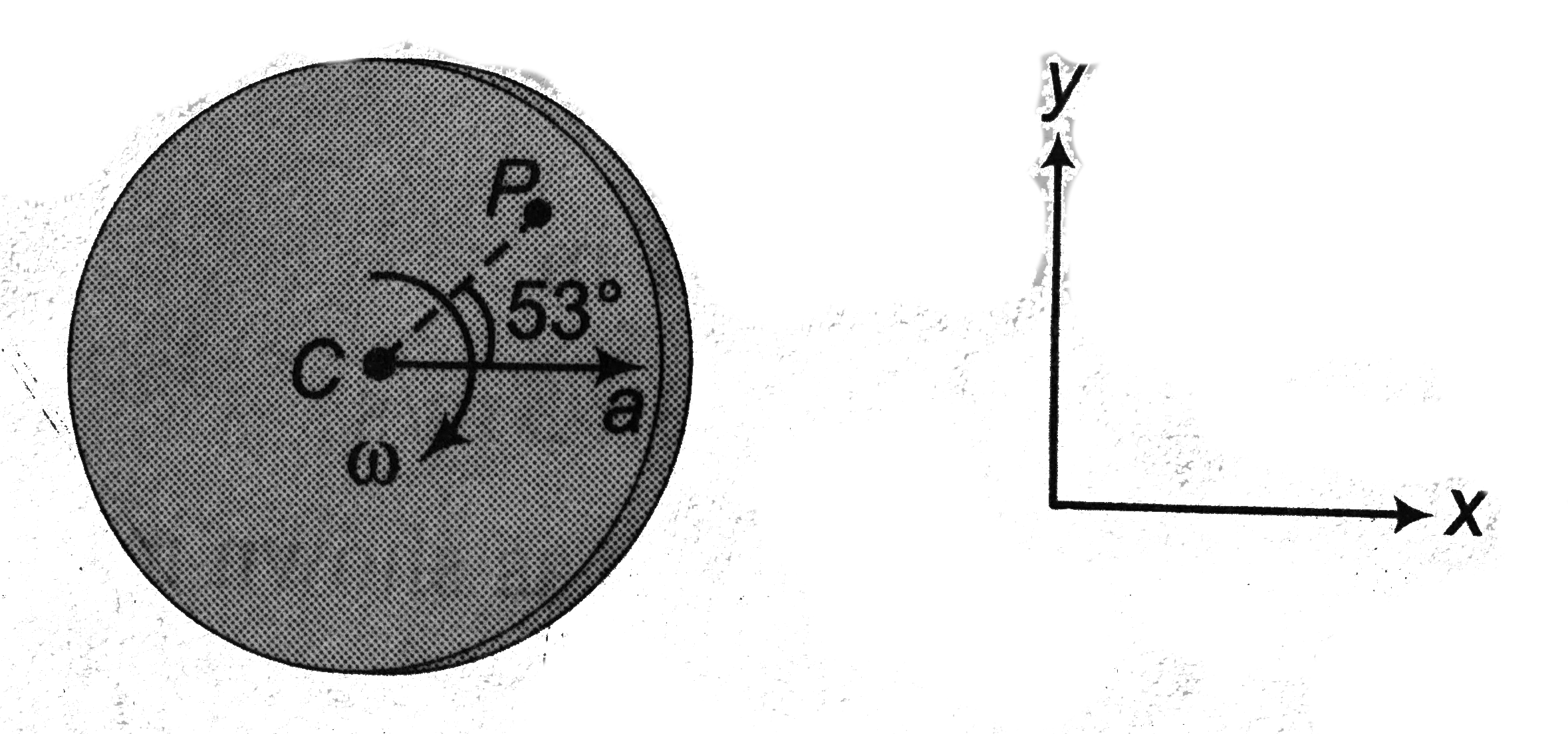
In the shown figure,
a=2m/s2,ω=(2t)rods−1 and CP=1m
In terms of ˆi and ˆj, find linear acceleration of the particle at P at P at t=1 s
View Solutiona. An atomic orbital has n=3. What are the possible values of l and m?
b. List the quantum numbers (mandl) of electrons for 3d orbital.
c. Which of the following orbitals are possible" 1p,2s,2p, and 3f?
View SolutionIf the sum of m terms of an A.P. is equal to the sum of either the next n terms or the next p terms, then prove that (m+n)(1m−1p)=(m+p)(1m−1n).
View SolutionThe first and last term of an A.P. are a and l respectively. If S be the sum of all the terms of the A.P., them the common difference is
View Solution
