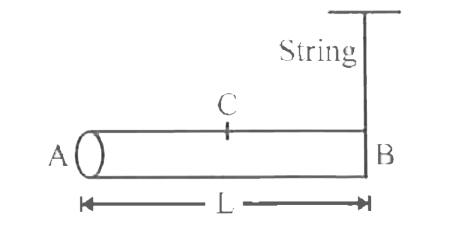
A homogeneous rod AB of mass m and length l leans with its lower end against the wall and is kept in the inclined positions by a string DC (Fig). The string is tied at point C to the wall and at point D to the rod so that . The angles formed by the string and the rod with the wall are and respectively. Find all possible values of the coefficient of friction between the rod and the wall.

Step by step video & image solution for A homogeneous rod AB of mass m and length l leans with its lower end against the wall and is kept in the inclined positions by a string DC (Fig). The string is tied at point C to the wall and at point D to the rod so that AD = AB//3. The angles formed by the string and the rod with the wall are alpha and beta respectively. Find all possible values of the coefficient of friction mu between the rod and the wall. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a masseless string tied to point Q as shown in Fig. When string is cut, the initial angular acceleration of the rod is :

View SolutionA uniform rod AB of length L and and weight Mg is hinged at one end A. The rod is kept in the horizontal position by a massless string. If the string is cut, then the angular acceleration of the rod will be
[M.I. of the rod about A is ML23]
View Solution
Knowledge Check
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the intial angular acceleration of the rod is
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3LA rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in the figure. When string is cut, the initial angular accleration of the rod is.
 A3g2LBgLC2gLD2g3L
A3g2LBgLC2gLD2g3LA uniform rod AB of length a hangs with one end against a smooth vertical wall, being supported by a string of length l, attached to the other end of the rod and to a point of the rod vertically above B. If the rod rests inclined to the wall at angle θ then cos2θ=
A(l2−a2)/a2B(l2−a2)/2a2C(l2−a2)/3a2Dnone of these
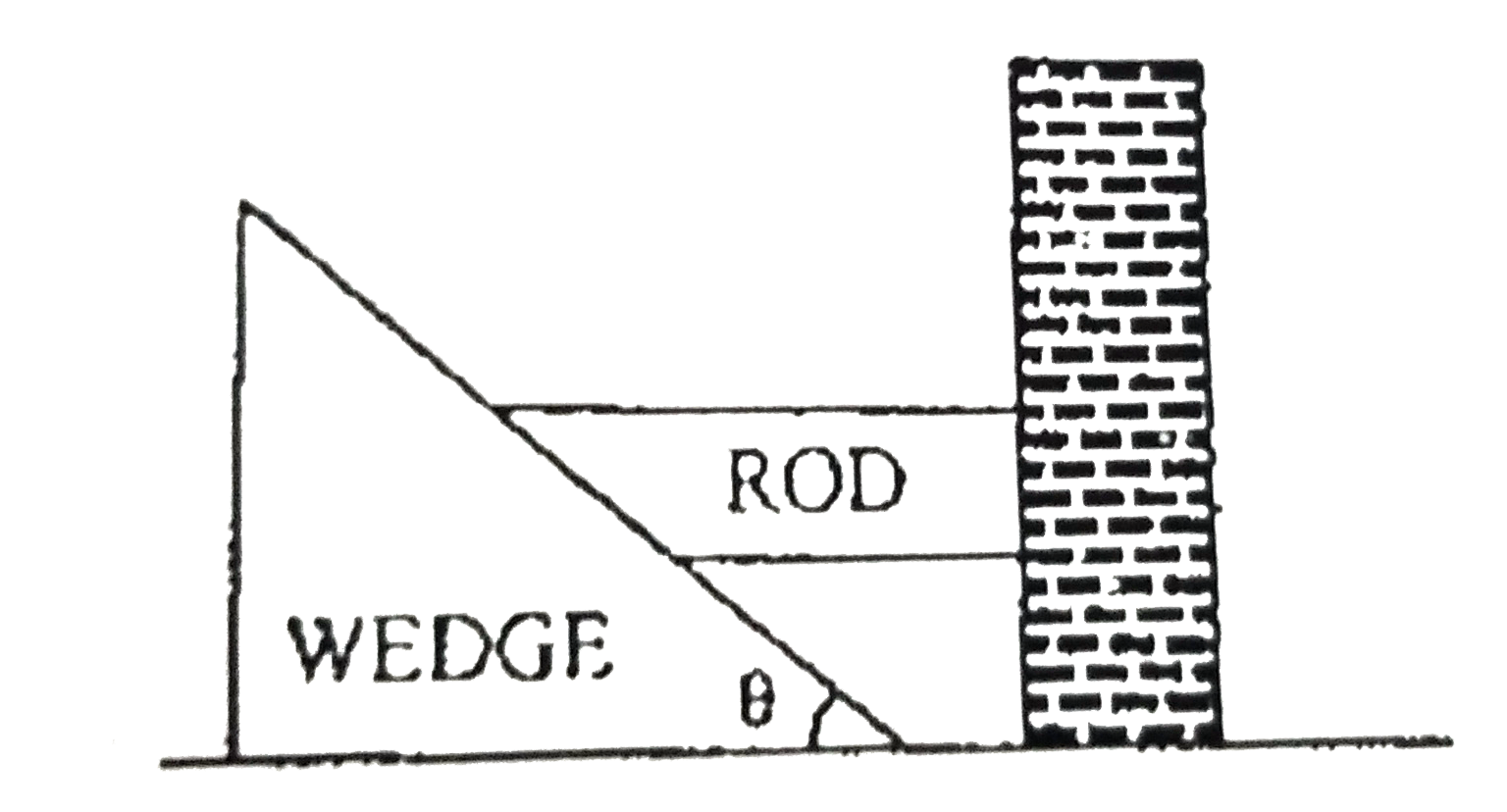
In the diagram shown, friction is present only between therod and the wall. The mass of the rod is M and tht of the wedge is 3M. What is the minimum value of the coefficient of friction between the rod and the wall so that rod remains in the state of rest?
View SolutionA uniform rod AB of mass 2kg is hinged at one end A. The rod is kept in the horizontal position by a massless string tied to point B. Find the reaction of the hinge (in N) on end A of the rod at the instant when string is cut. (g=10m/s2)

View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the

Normal reaction by ground on the rod
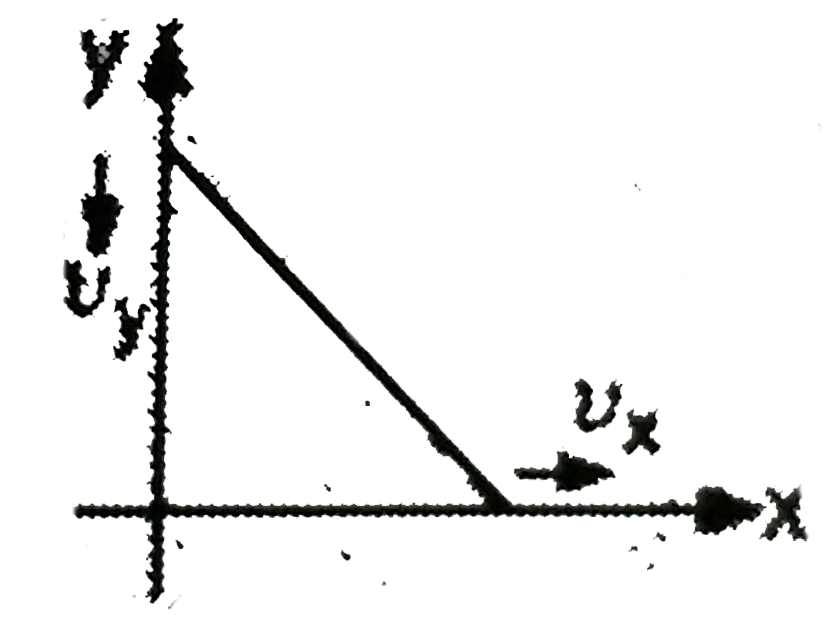
View SolutionA rod of length I leans by its upper end against a smooth vertical wall, while its other end leans against the floor. The end that leans against the wall moves uniformly downward. Then:
View SolutionA uniform rod of mass m and length l is hanged by two stirngs as shown in figure. Suddenly one string is cut. The tension in other string at this instant is

View Solution
