Two blockM1 and M2 rest upon each other on an inclined plane Coefficient of friction between surfaces are shown if the angle 0 is slowly increased and M1≤M2 then
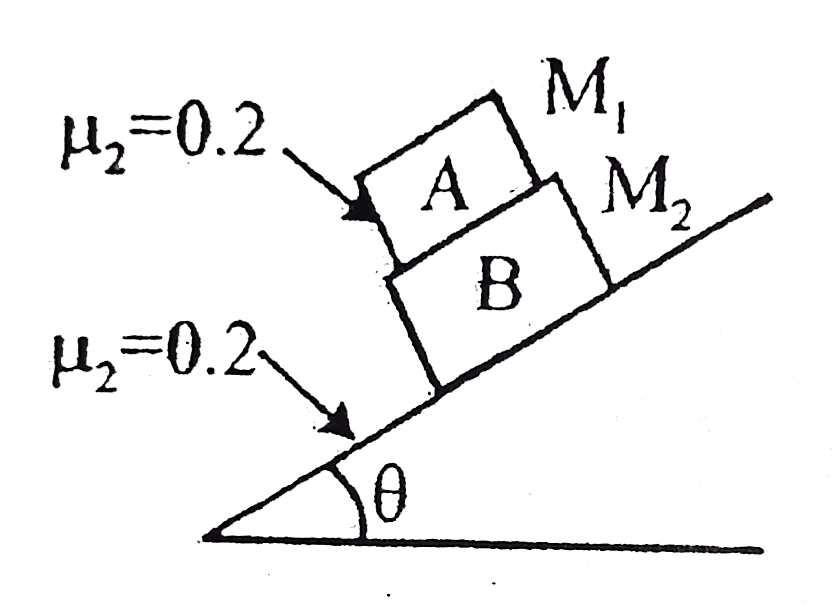
block A slips first
block B slips first
both slip simultaneously
both remain at rest
The correct Answer is:B
Step by step video, text & image solution for Two block M_(1) and M_(2) rest upon each other on an inclined plane Coefficient of friction between surfaces are shown if the angle 0 is slowly increased and M_(1) le M_(2) then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension134videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
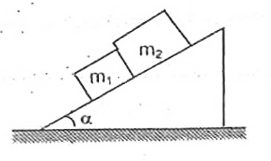
Two blocks of masses m1andm2 are kept touching each other on a rough fixed inclined plane of inclination α. Coefficients of kinetic friction between the inclined plane and the block m1 is k1 and between the inclined plane and block m2 is k2. Find the force of interaction between the blocks in the process of motion.
 View Solution
View SolutionThe coefficient of friction between m2 and inclined plane is μ (shown in the figure). If m1m2=sinθ then
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m rests on a rough inclined plane. The coefficient of friction between the surface and the block is µ. At what angle of inclination θ of the plane to the horizontal will the block just start to slide down the plane?
Aθ=tan−1μBθ=cos−1μCθ=sin−1μDθ=sec−1μ - Question 2 - Select One
Two blocks of masses m1 and m2 are placed in contact with each other on a horizontal platform. The coefficient of friction between the platform and the two blocks is the same. The platform moves with an acceleration. The force of interaction between the blocks is :
 Azero only if m1=m2Bzero in all casesCnon - zero only if m1>m2Dnon - zero only if m1<m2
Azero only if m1=m2Bzero in all casesCnon - zero only if m1>m2Dnon - zero only if m1<m2 - Question 3 - Select One or More
A block of mass m in the equilib rium on a rough inclined plane with inclination α and coefficient of friction as shown in the figure (μ<tanα). A force F is applied on the block which makes an angle θ with the horizontal as shown in diagram.
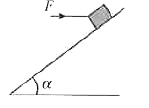 ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
ANormal force on the block mgcosα+Fsinθ.BMinimum force f to keep the blockin equilibrium Fmin=mg(sinα−μcosα)2μ√1+μ2Cμ=tanθDNone of these
Two blocks of masses M1 and M2 connected by a light spring rest on a horizontal plane . The coefficient of friction between the blocks and the surface is equal to μ . The minimum constant force that has to be applied in the horizontal direction to the block of mass M1 in order to shift the other block is (M1+M2α)μg , then α is :
View SolutionTwo blocks of masses m1amdm2 connected by a string and placed on an rough inclined plane having coefficient of friction μ is shown in fig 7.89 Find the retio of masses m1/m2 so that

a. the block m1 start moving downward
b. the block m1 start moving upwnward
c. no motion takes planeView SolutionTwo blocks of masses m1 and m2 kept touching each other on an inclined plane of inclination a with the horizontal. Show that (i) theforce of interaction between the blocks is (μ1−μ2)m1m2gcosα(m1+m2) and (ii) the minimum value of α at which the blocks just start sliding is a=tan−1.μ1m1+μ2m2m1+m2 . Where μ1 and μ2 are the coefficients of friction between the block m1 and the inclined plane and between the block m2 and the inclinedplane respectively.
View SolutionTwo blocks of masses m1 and m2 are connected by a spring of stiffness k. The coefficient of friction between the blocks and the surface is μ. Find the minimum constant force F to be applied to m1 in order to just slide the mass m2.
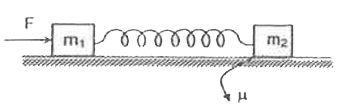 View Solution
View SolutionTwo blocks of mass m1 and m2(m2>m1) are placed in contact with each other on an inclined plane as shown in figure . The coefficient of friction between m1 and surface is μ1 and between m2 and surface is μ2.


 View Solution
View Solution

