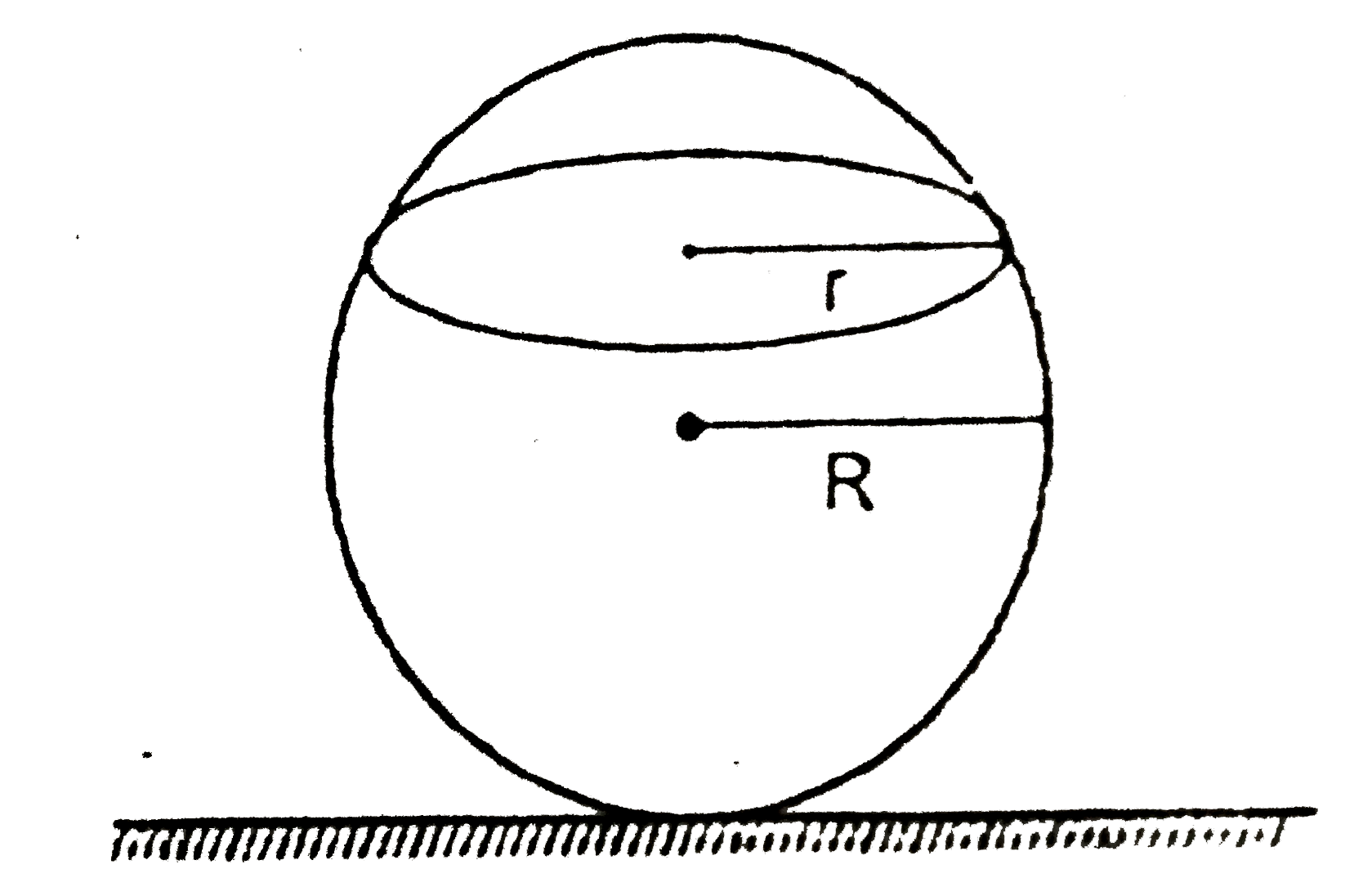
A circular rope of weight W and radius r=R2 is resting on a smooth sphere of radius R The tension in rope is

W/(π√6)
W/(π√12)
W/(π√10)
none of these
The correct Answer is:B
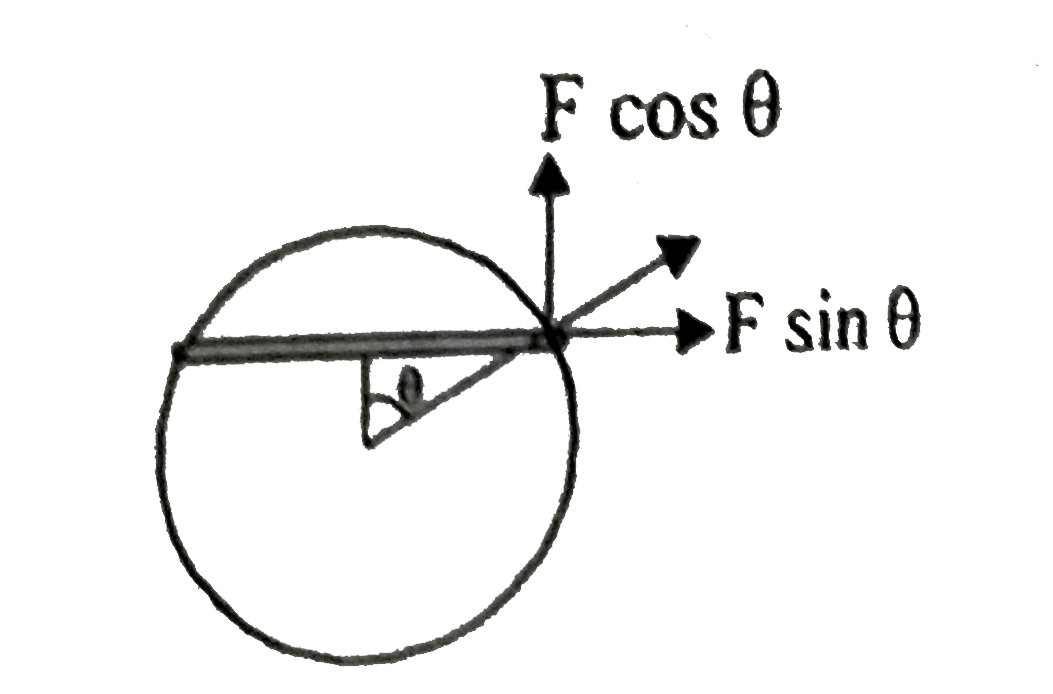
fsinθ=T(2π)
Fcosθ=W
tanθ=T(2π)w
T=Wtanθ2π=wtan30∘2π=wπ√12
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension134videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
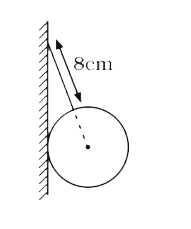
A uniform sphere of weight W and radius 5 cm is being held by string as shown in the figure. The tension in the string will be
 View Solution
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The volume of a sphere of radius 2r is
A32πr33B16πr33C8πr33D64πr33 - Question 2 - Select One
The radius of gyration of a sphere of radius R about a tangent is.
A√23RB√25RC√53RD√75R - Question 3 - Select One
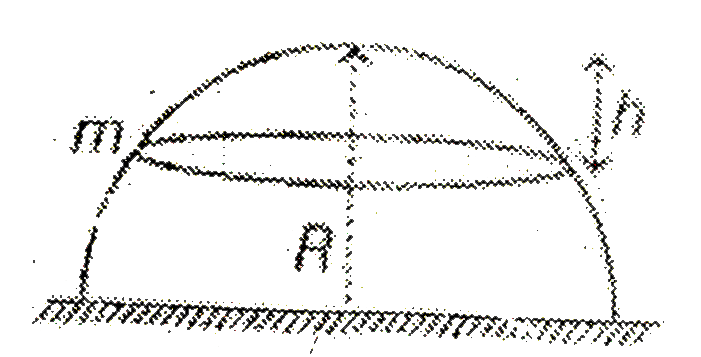
A unofrom rope of mass m is placeced on a smooth fixed sphere of radius R as shown in the figure .Find the tension T in the rope when it is in a horizontal plane at a vertical distance h=R/2 below the top of the sphere .
 Amg2πBmg2C√3mg2D√3mg2π
Amg2πBmg2C√3mg2D√3mg2π
A cylinder of weight W and raidus R is to be raised onto a horizontal step of height h=R/3 as shown. A rope is wrapped around the cylinder and pulled horizontally. Assuming no slipping, find the minimum value of F to raise the cylinder.
 View Solution
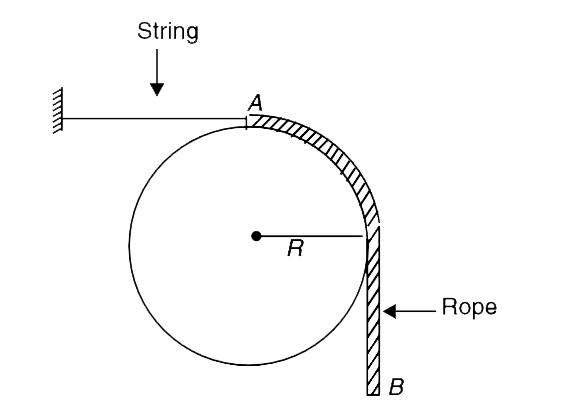
View SolutionA rope of length (π2+1) R has been placed on a smooth sphere of radius R as shown in figure. End A of the rope is at the top of the sphere and end B is overhanging. Mass per unit length of the rope is λ . The horizontal string holding this rope in place can tolerate tension equal to weight of the rope. Find the maximum mass (M0) of a block that can be tied to the end B of the rope so that the string does not break.
 View Solution
View SolutionA uniform circular chain of radius r and mass m rests over a sphere of radius R as shown in figure. Friction is absent everywhere and system is in equilibrium . Find the tension in the chain.
 View Solution
View SolutionA right circular cone of radius R and height 2R is placed on a hemisphere of radius R. Locate c.m. of the combined mass from O.
 View Solution
View SolutionA thin circular ring of mass per unit length p and radius r is rotating at an angular speed ω as shown in figure. The tension in the ring is
 View Solution
View Solution

