A small bead of mass m can moves on a smooth circular wire (radiusR) under the action of a force F=kmr2 directed (r=position of bead from P&K=constant) towards a point P with in the circle at a distance R2 from the centre what should be the minimum velocity of bead at the point of the wire nearest the centre of force (P) so that bead will complete the circle

√3kR
√8k3R
√6kR
none of these
The correct Answer is:B
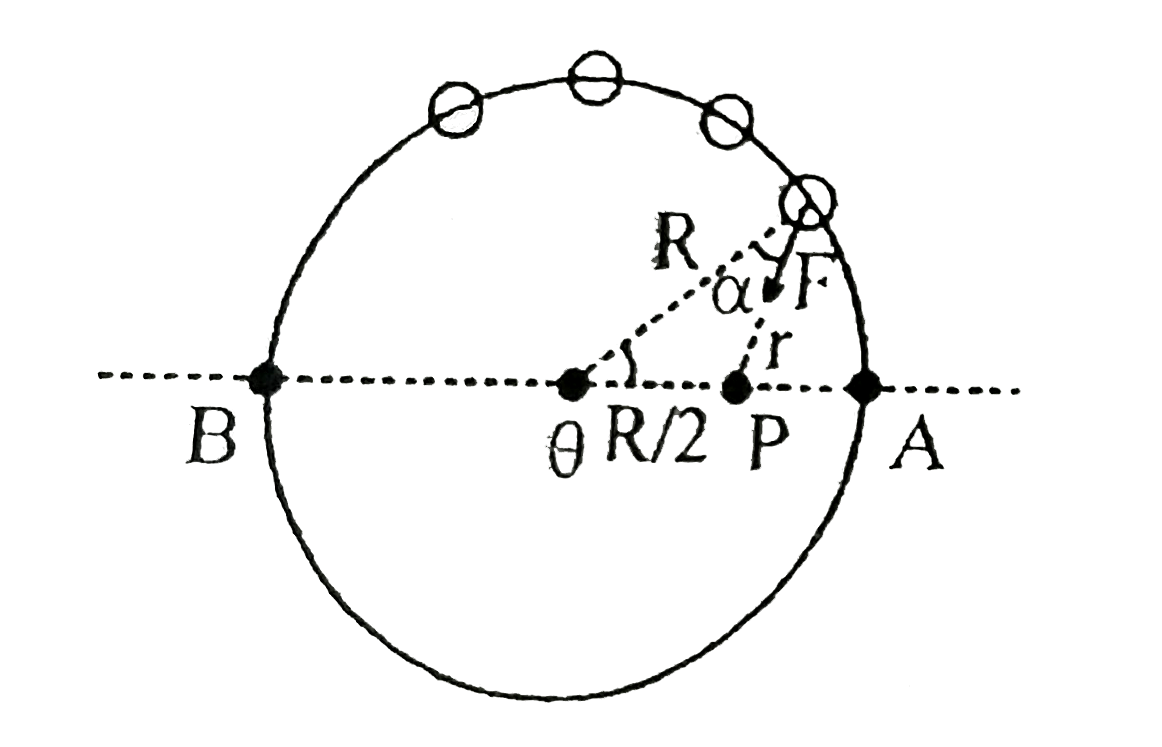
value of A at any angular position 'theta' is given by
f=kmr2 here is given by
r=√(Rcosθ−R/2)2+(Rsinθ)2=√R2+R2/4−R2cosθ=R2√5−4cosθ
Also2sinαR=sin0ri.esinα=sinθ√5−4cosθ
for small angular displacement 'dtheta' work done by this force dw =-frd0cos(9theta-alpha)=-fR sin alpha dtheta
4kmRR2(5−4cosθ)sinθ√5−4cosθdthη
work done in moving bead from AtoB
Δw=−4kmRπ∫θsinθdθ(5−4cosθ)3/2=−kmRπ∫θ4sinθdθ(5−4cosθ)3/2
=kmR9∫θdtt3/2=−kmR∣∣∣t−1/2−(1/2)∣∣∣91
=+2kmR(13−1)=−43kmR
:.Energy provided at point A most be equal to this work done
∴12mv2m=43kmR⇒vmin=√8k3R
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension
134 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
A uniform circular plate of radius 2R has a circular hole of radius R cut out of it. The centre of the smaller circle is at a distance of R/3 from the centre of the larger circle. What is the position of the centre of mass of the plate?
View SolutionA small ball of mass m is released in a smooth circular tube as shown in figure. The minimum height h such that bead can complete the circle is
View Solution
Knowledge Check
A small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?
 AvRB2vRCv2RD3vR
AvRB2vRCv2RD3vRA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction
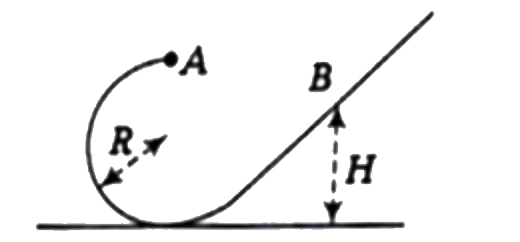 ARB2 RC3R2D5R2
ARB2 RC3R2D5R2Two beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.
 What is the coefficient of restituting between the beads?A1B12C13D1√2
What is the coefficient of restituting between the beads?A1B12C13D1√2
A small bead of mass m moving with velocity v gets threaded on a stationary semicircular ring of mass m and radius R kept on a horizontal table. The ring can freely rotate about its centre. The bead comes to rest relative to the ring. What will be the final angular velocity of the system?

View SolutionA small bead of mass M slides on a smooth wire that is bent in a circle of radius R. It is released at the top of the circular part of the wire (point A in the figure) with a negligibly small velocity. Find the height H where the bead will reverse direction

View SolutionTwo beads A and B of masses m1 and m2 respectively, are threaded on a smooth circular wire of radius a fixed in a vertical plane. B is stationary at the lowest point when A is gently dislodged from rest at the highest point. A collided with B at the lowest point. The impulse given to B due to collision is just great enough to carry it to the level of the centre of the circle while A is immediately brought to rest by the impact.
 What is the coefficient of restituting between the beads?
What is the coefficient of restituting between the beads?
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.

If v=2u0, the tension T in th elastic string when the bead is at the highest point B of the wire is
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
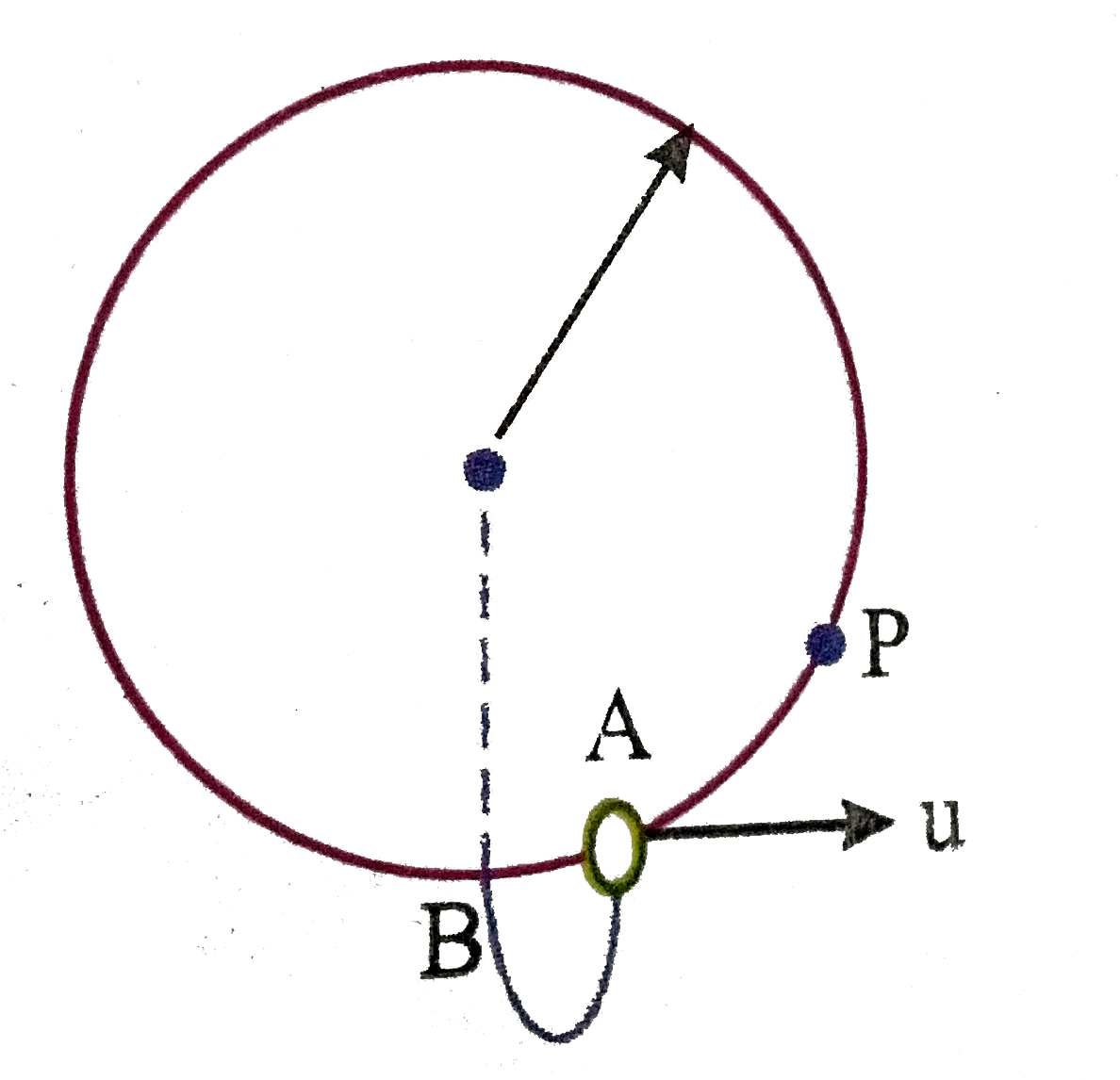
The smallest value u0 of u for which the bead will make complete revolutions of the wire will be
View Solution
