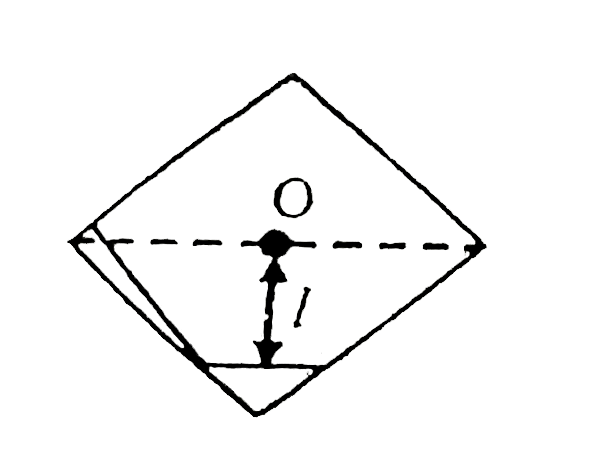
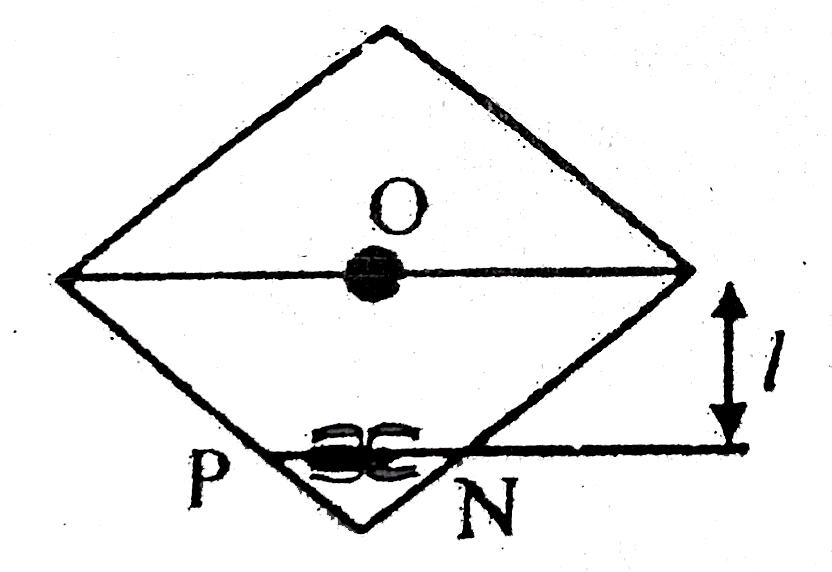
A square metal frame in the vertical plane is hinged at O at its center a bug moves along the rod PN which is at a distance l from the hinge such that the whole frame is always stationary even though the frame is free to ratate in the verticle plane about the hinge then the motion of the bug will be simple harmonic with time period
2π√lg
2π√2lg
2π√4lg
2π√l2g
The correct Answer is:A
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Comphrehension134videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
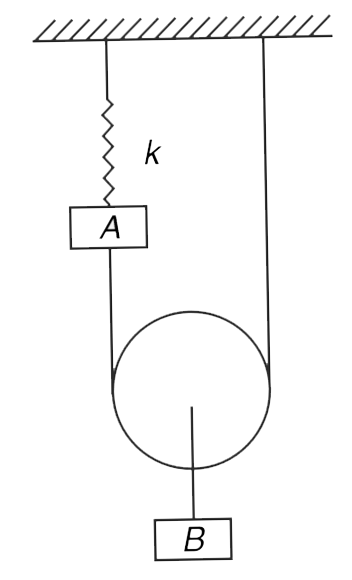
(i) In the system shown in figure, find the time period of vertical oscillations of the block A. Both the blocks A and B have equal mass of m and the force constant of the ideal spring is k. Pulley and threads are massless
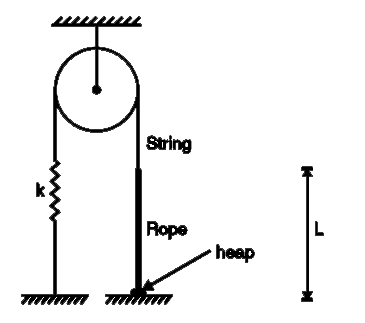
(ii) In the arrangement shown in the figure the spring, string and the pulley are mass less. The force constant of the spring is k. A rope of mass per unit length equal to λ(kgm−1) hangs from the string as shown. In equilibrium a length L of the rope is in air and its bottom part lies in a heap on the floor. The rope is very thin and size of the heap is negligible though the heap contains a fairly long length of the rope. The rope is raised by a very small distance and released. Show that motion will be simple harmonic and calculate the time period. Assume that the hanging part of the rope does not experience any force from the heap or the floor (For example there is no impact force while the rope hits the floor while moving downward and there is no impulsive pull when the vertical part jerks a small element of heap into motion).
 View Solution
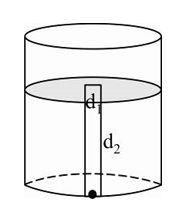
View SolutionA thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A uniform rod of mass m and length l is fixed from Point A, which is at a distance l/4 from one end as shown in the figure. The rod is free to rotate in a vertical plane. The rod is released from the horizontal position.

What is the reaction at the hinge, when kinetic energy of the rod is maximum?A47B57mgC137mgD117mg - Question 2 - Select One
A wire frame in the shape of an equilateral triangle is hinged at one vertes so that it can swing freely in a vertical plane, with the plane of the Δ always remaining vertical. The side of the frame is 1/√3m. The time period in secods of small oscillations of the frmae will be-
Aπ√2Bπ√2Cπ√6Dπ√5 - Question 3 - Select One
A disc is hinged such that it can freely rotate in a vertical plane about a point on its radius. If radius of disc is 'R' , then what will be minimum time period of its simple harmonic motion ?
A2π√RgB2π√3R2gC2π√√2RgD2π√R2g
A thin rod of length L and area of cross section S is pivoted at its lowest point P inside a stationary, homogeneous and non-viscous liquid. The rod is free to rotate in a vertical plane about a horizontal axis passing through P. The density d1of the rod is smaller than the density d2 of the liquid. The rod is displaced by a small angle theta from its equilibrium position and then released. Shown that the motion of the rod is simple harmonic and determine its angular frequency in terms of the given parameters ___________ .
 View Solution
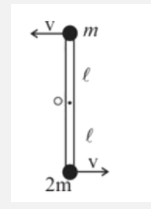
View SolutionTwo particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
 View Solution
View SolutionAn L shaped frame is free to rotate in a vertical plane about a horizontal axis passing through a smooth hinge O. Each side of the frame has a length L and mass m. Frame is let to fall with one side horizontal and the other vertical.

With what speed the end A will strike the ground ?View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
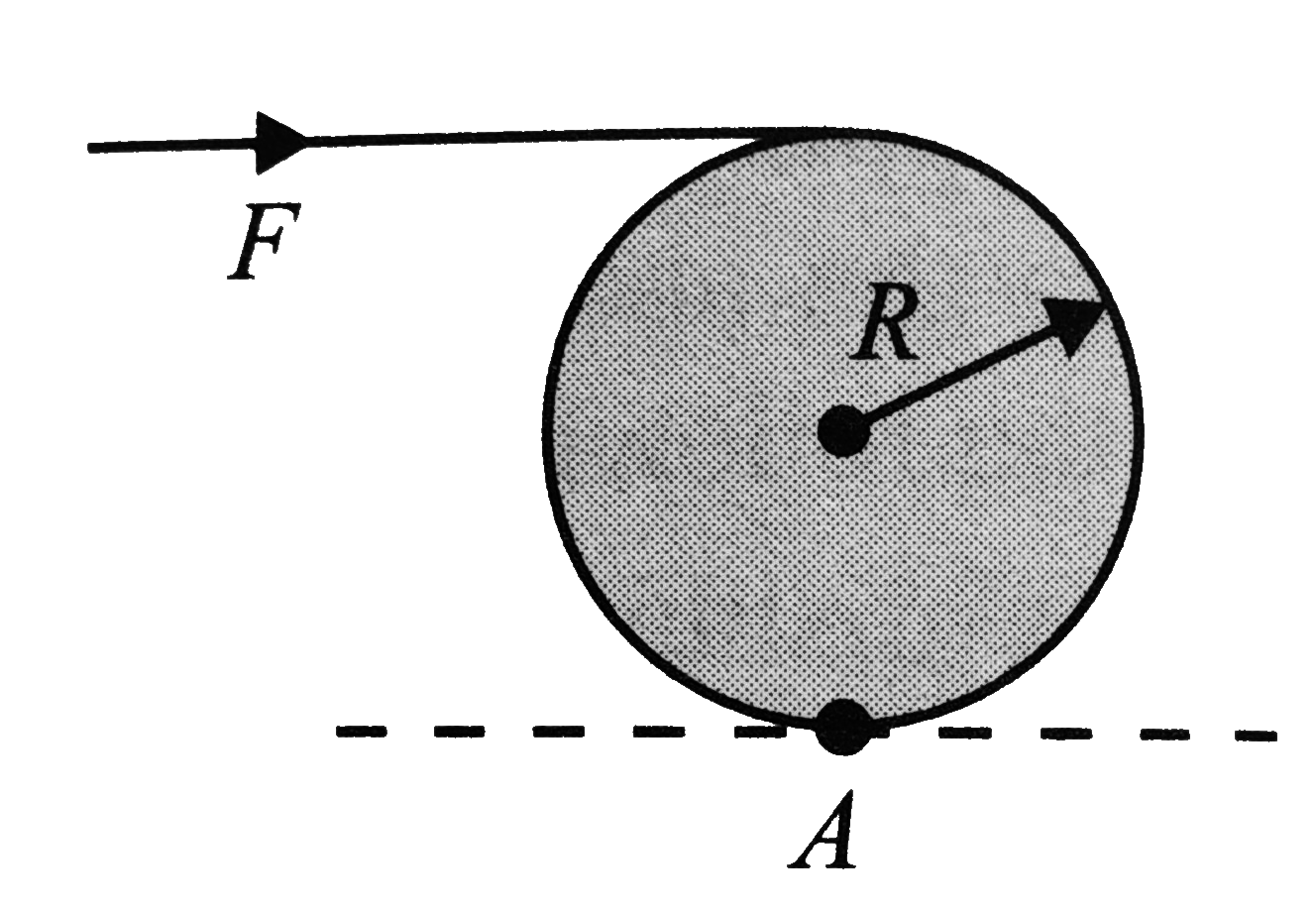
Component of reaction at the hinge in the vertical direction isView SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
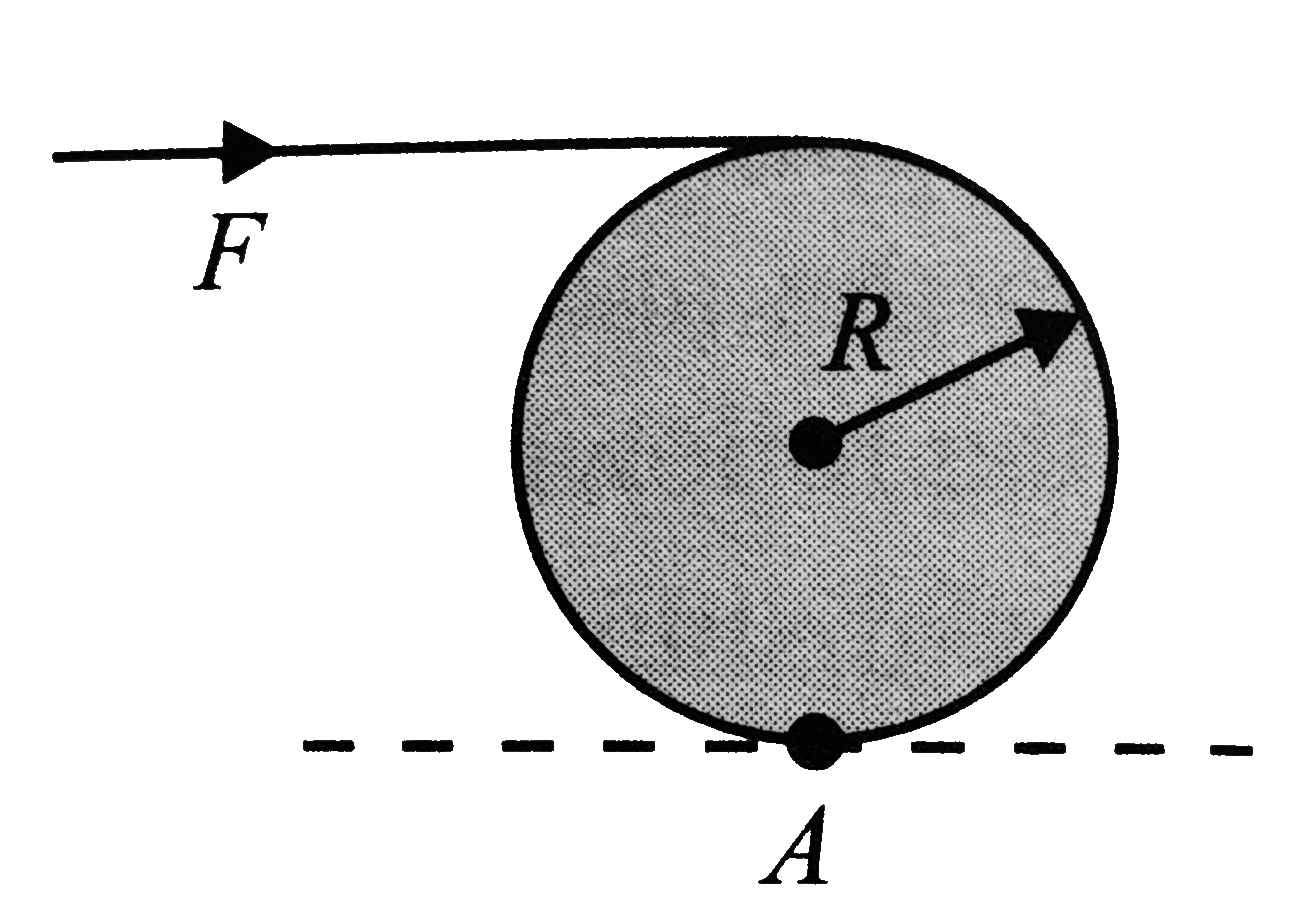
Component of reaction at the hinge in the horizontal direction isView Solution