Two satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.
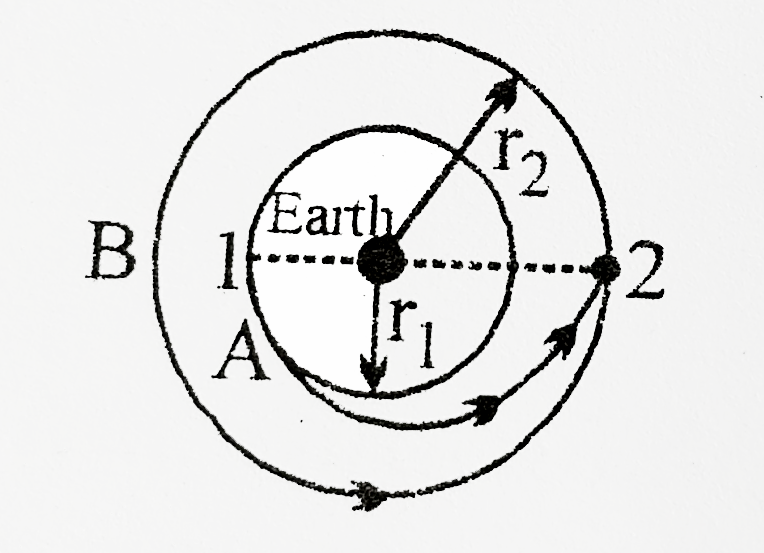
For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If r2=3r1 and time period of revolution for B be T than time taken by A in moving from position 1 to position 2
A,B and earth's centre are in same straight line
B is ahead of A angularly
B is behing A angularly
none of these
The correct Answer is:B
Step by step video, text & image solution for Two satellites A and B are revolving around the earth circular orbits of radius r_(1) and r_(2) respectively with r_(1) lt r_(2). Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together. For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T^(2)alpha r^(3) where a is semi major axis of the ellipse which is (r_(1)+r_(2))/(2) in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre. If r_(2)=3r_(1) and time period of revolution for B be T than time taken by A in moving from position 1 to position 2 by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
Two satellites of mass MA and MB are revolving around a planet of mass M in radius RA and RB respectively. Then?
View Solution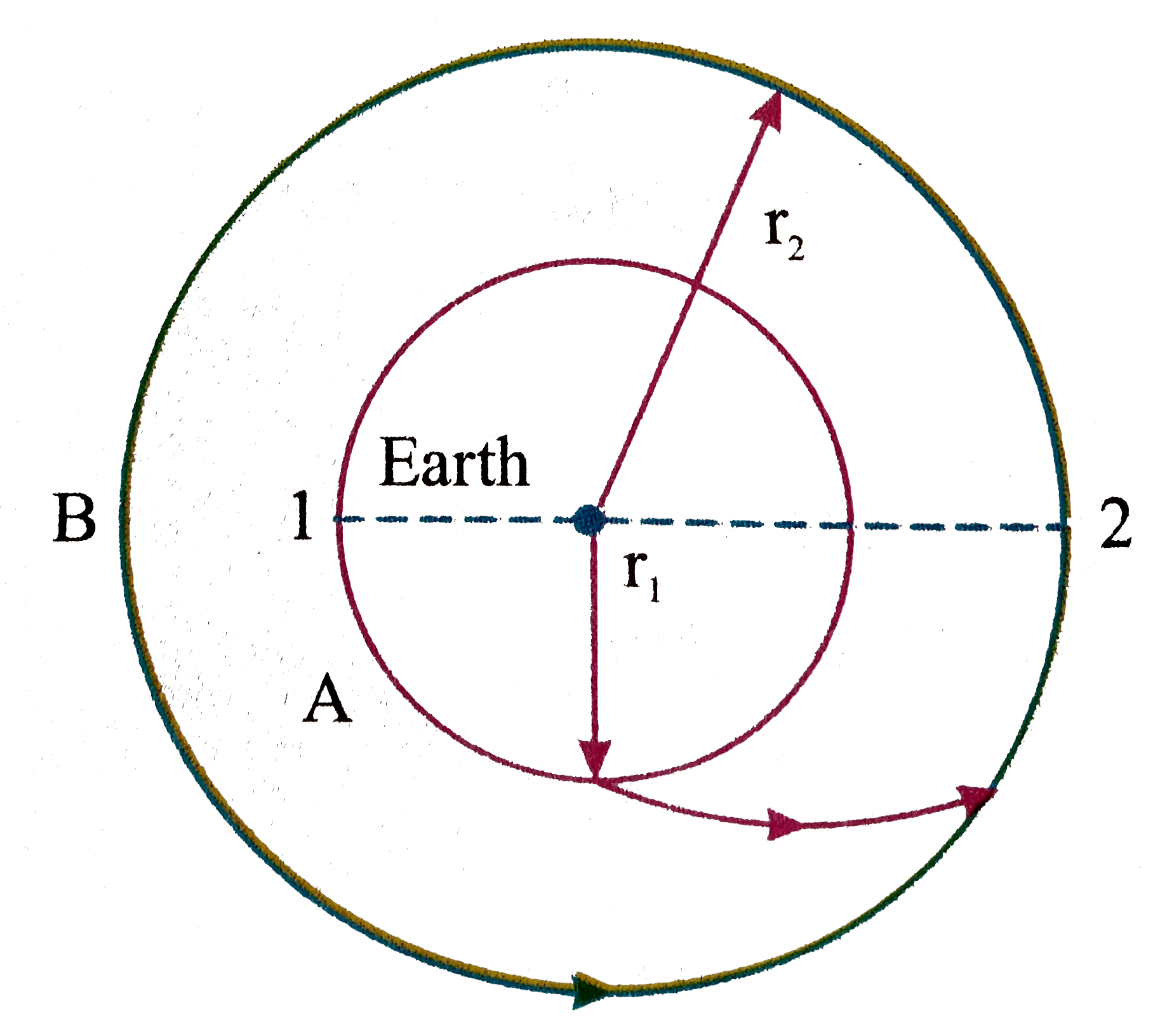
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If the two have same mass
View Solution
Knowledge Check
Two satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.
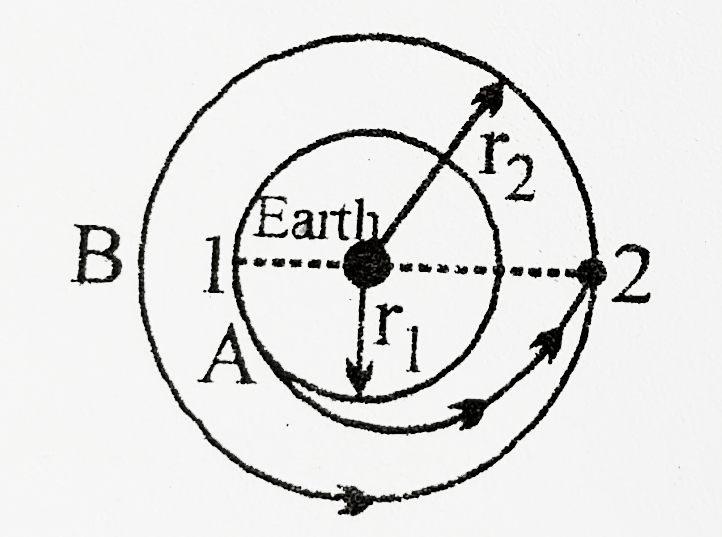
For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
If the two have same massAA would have more potential energy than B while on their B while on their initial circular paths.BA would have more kinetic energy than B while on their initial circular paths.CRelative to Earth's centre, angular momentume of A when it is in elliptical path would be less than angular momentum of B.DDuring the whole process angular of B T than taken by A in moving from position 1 to position 2Two satellites A and B are revolving around the earth circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. A?t position 2, A is given another impluse so that velocities of A and B at 2 become equal and the move together.
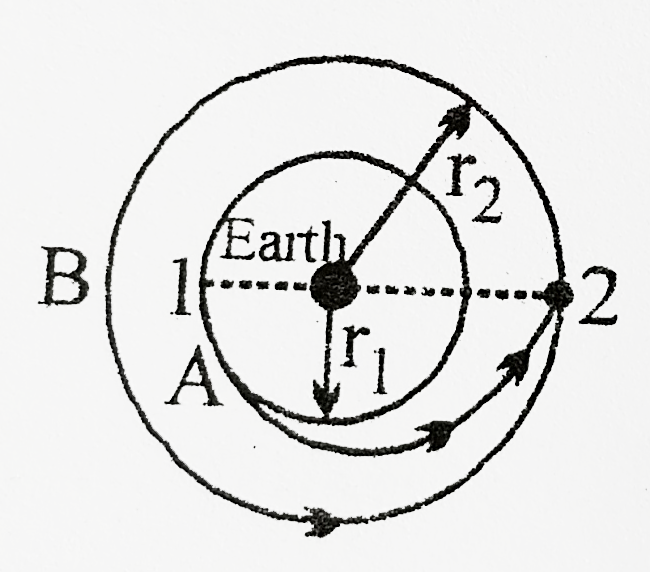
For any elliptical path of the satellite of the time period of revolution is given by Kepler's planetary law as T2αr3 where a is semi major axis of the ellipse which is r1+r22 in this case. Also angular mopmentum of any satellite revolving around the Earth will remain a constant about EArth's centre as force of gravity on the satellite which keeps it in elliptical path is along its position vector relative to the earth centre.
When A is given its first impulse at the moment.AA, B and earth centre are in same straight lineBB is ahead of A angularlyCB is behind A angularDNone of these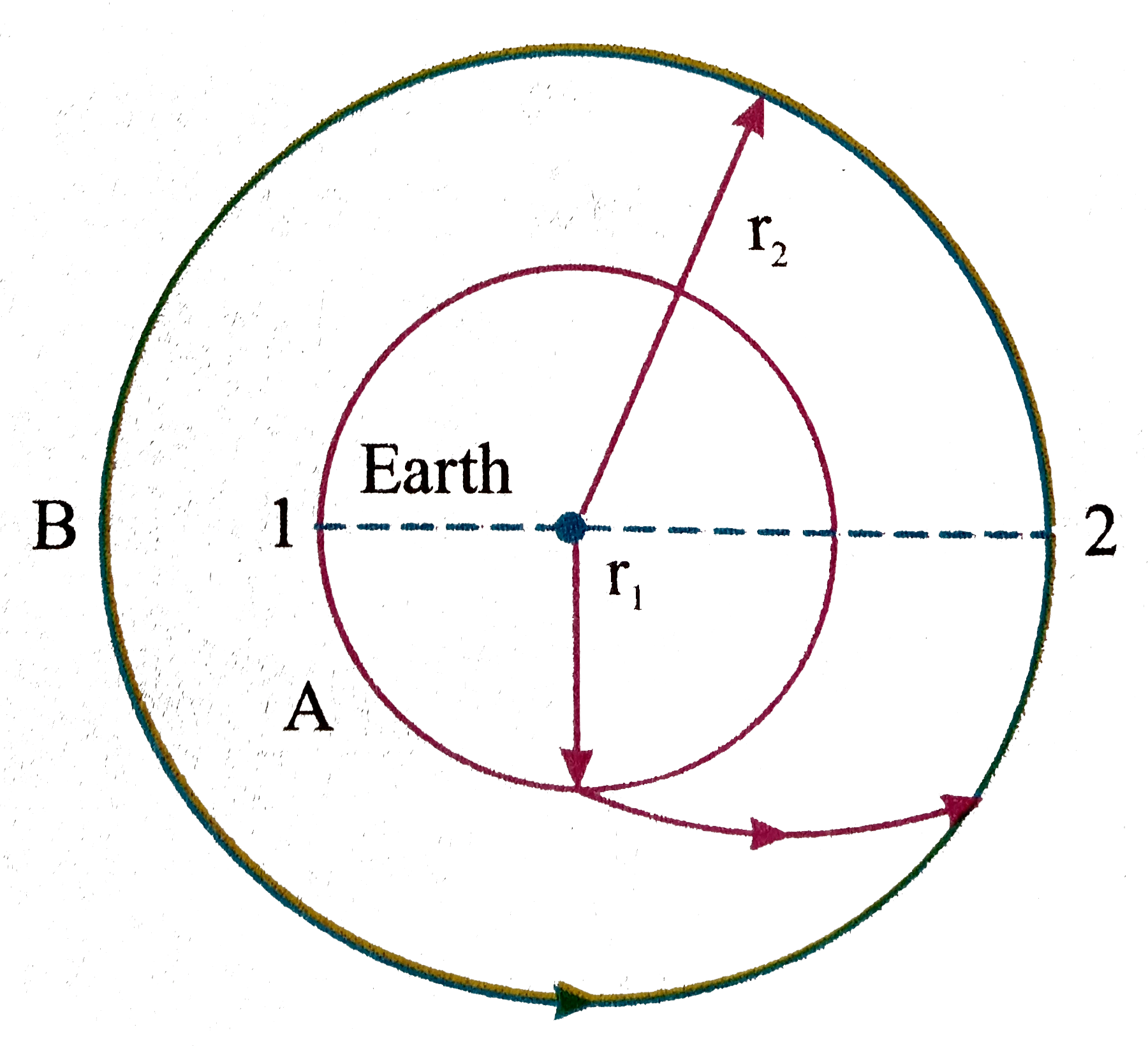
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
If r2=3r1 and time period of revolution for B be T then time taken by A in moving from position 1 to position 2 isAT√3√2BT√32CT√23√3DT√23
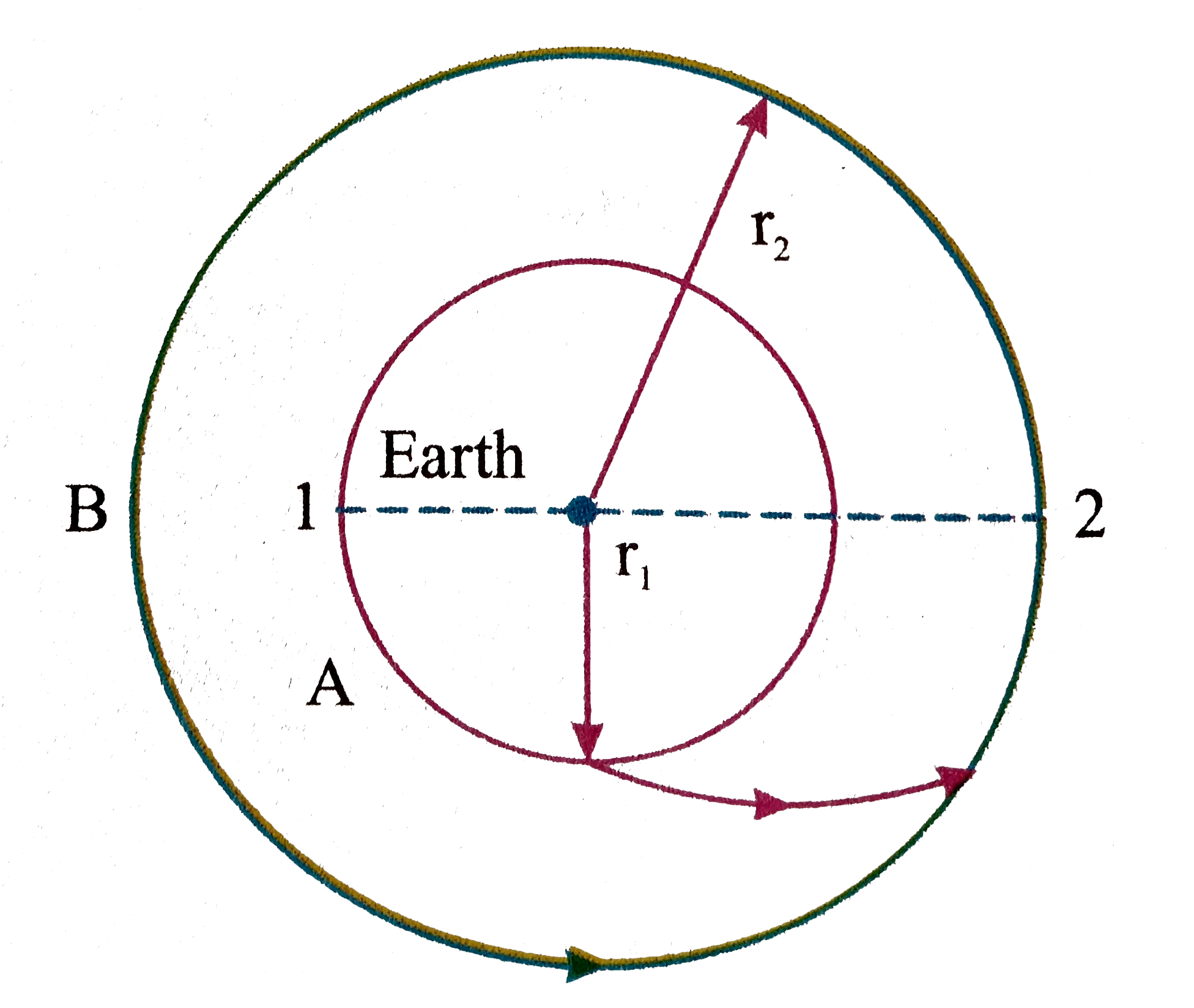
Two satellites A and B are revolving around the earth in circular orbits of radius r1 and r2 respectively with r1<r2. Plane of motion of the two are same. At position 1, A is given an impulse in the direction of velocity by firing a rocket so that it follows an elliptical path to meet B at position 2 as shown. focal lengths of the elliptical path are r1 and r2 respectively. at position 2, A is given another impulse so that velocities of A and B at 2 become equal and the two move together. for any elliptical path of the satellite time period of revolution is given Kepler's planetry law as T2αr3 where a is semi-major axis of the ellipse which is r1+r22 in this case. also angular momentum of any satellite revolving around the earth will remain a constant about earth's centre as force of gravity on the satellite which keeps it in elliptical path is given its position vector relative to the earth centre.
When A is given its first impulse at that moment
View SolutionSatellites A and B are orbiting around the earth in orbits of ratio R and 4R respectively. The ratio of their areal velocities is-
View SolutionTwo satellite are revolving around the earth with velocities v1 and v2 and in radii r1 and r2(r1>r2) respectively. Then
View SolutionTwo particles of equal masses are revolving in circular paths of radii r1 and r2 respectively with the same speed. The ratio of their centripetal force is
View SolutionTwo satellites of masses 50 kg and 100 kg revolve around the earth in circular orbits of radii 9 R and 16 R respectively, wehre R is the radius of earth. The speeds of the two satellites will be in the ratio
View Solution
