You are to conduct a series of trials. For each trial the inclination of the plane is set to an angle theta, ranging from 0∘→90∘ and an object is released from rest at the top of the stationary inclined plane. The coefficient of static friction between the object and the inclined plane is μs. In each case below, predict the observed outcome for the trial. In the following equation 'tumble' means 'tip' over and rotate' and 'sliding' means NO tumbling Case3 : The object is a cube and mu_(s) is very large (μ>>1)
the cube will remain at rest for small theta and slide down only for theta greater than a certain non-zero value
The cube will stay on the incline as if it were glued to it, for all θ
The cube will move relative to the inclined plane only for θ=90∘
The cube will tumble down only for θ>45∘
The correct Answer is:D
Topper's Solved these Questions
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning
75 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective
131 Videos
- MASTER PRACTICE PROBLEMBOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic
70 Videos
- FLUID MECHANICSBOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE
10 Videos
- SEMICONDUCTORSBOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question
32 Videos
Similar Questions
The coefficient of friction between the block and the inclined plane is μ.
View SolutionA small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.
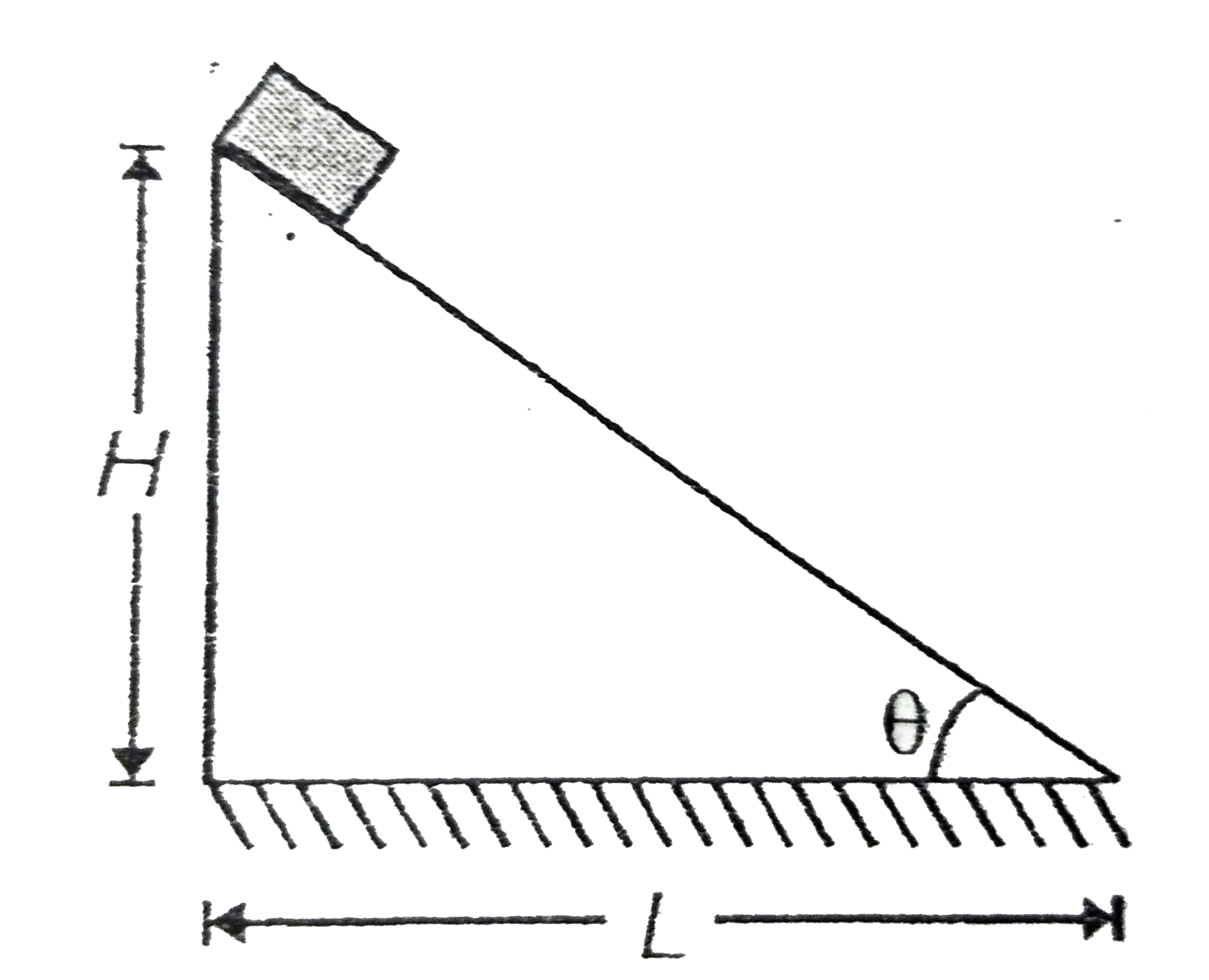
View Solution
Knowledge Check
You are to conduct a series of trials. For each trial the inclination of the plane is set to an angle theta, ranging from 0∘→90∘ and an object is released from rest at the top of the stationary inclined plane. The coefficient of static friction between the object and the inclined plane is μs. In each case below, predict the observed outcome for the trial. In the following equation 'tumble' means 'tip' over and rotate' and 'sliding' means NO tumbling Case1: The object is a sphere and μs=0
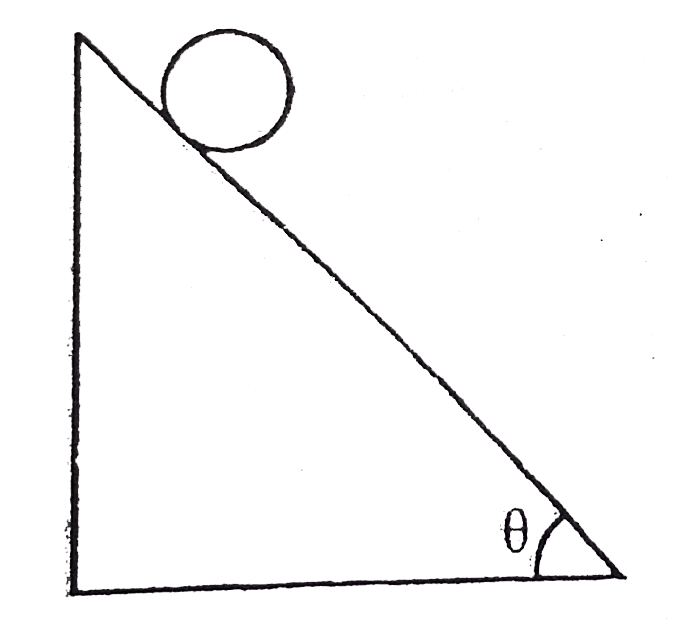 AThe sphere will roll without slipping for small θ and slide down only for θ greater than a certain non-zero valueBThe sphere will remain at rest for small θ and roll without slipping only for θ greater than a certain non-zero valueCThe sphere will slide down for all θ>0∘DThe Sphere will roll without slipping for all θ>0∘
AThe sphere will roll without slipping for small θ and slide down only for θ greater than a certain non-zero valueBThe sphere will remain at rest for small θ and roll without slipping only for θ greater than a certain non-zero valueCThe sphere will slide down for all θ>0∘DThe Sphere will roll without slipping for all θ>0∘You are to conduct a series of trials. For each trial the inclination of the plane is set to an angle theta, ranging from 0∘→90∘ and an object is released from rest at the top of the stationary inclined plane. The coefficient of static friction between the object and the inclined plane is mu_(s). In each case below, predict the observed outcome for the trial. In the following equation 'tumble' means 'tip' over and rotate' and 'sliding' means NO tumbling Case2 : The object is a cube and μs=0 In this experiment, the angle theta is varied only between 0^(@) and 45^(@)
 AThe cube will slide down for all 45∘>θ>0∘BThe cube will remain at rest for small theta and slide down only for theta greater then a certain non-zero valueCThe cube will roll without slipping for all 45∘>θ>0∘DThe cube will tumble down for all 45∘>θ>0∘
AThe cube will slide down for all 45∘>θ>0∘BThe cube will remain at rest for small theta and slide down only for theta greater then a certain non-zero valueCThe cube will roll without slipping for all 45∘>θ>0∘DThe cube will tumble down for all 45∘>θ>0∘A block is stationary on an inclined plane If the coefficient of friction between the block and the plane is μ then
 .Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
.Aμ>tanθBf=mgsinθCf=μmgcosθDthe reaction of the ground on the block is mg cos θ
A small blockofmass 'm' is released from rest at the top of a rough inclined plane as shown The coefficient of friction between the block and inclined plane is 'μ' Using work-energy theorem, find the speed of block as it passes the lowest point.

View SolutionA uniform disc is released from the top of a rough inclined plane of angle θ and height h. The coefficient of friction between the disc and the plane is μ=tanθ4. The speed of centre of mass of disc on reaching the bottom of the plane is
View SolutionIf the angle of inclination of the inclined plane is sin−1(12) when the body just starts sliding find the angle of repose and coefficient of static friction between the body and the inclined plane.
View SolutionAn object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
View SolutionAn object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
View Solution
