A beam of electrons has radius r and contains 'n' electrons per cubic meter moving with velocity along the beam (figure). Assume that a beam that is much longer than its diameter forms a cylinderically symmetric distribution of charge and current. The beam expands if the electric force exceeds the magnetic force. So long as the expansion is slow, the approximations of cylindrical symmetry and static fields remain valid.
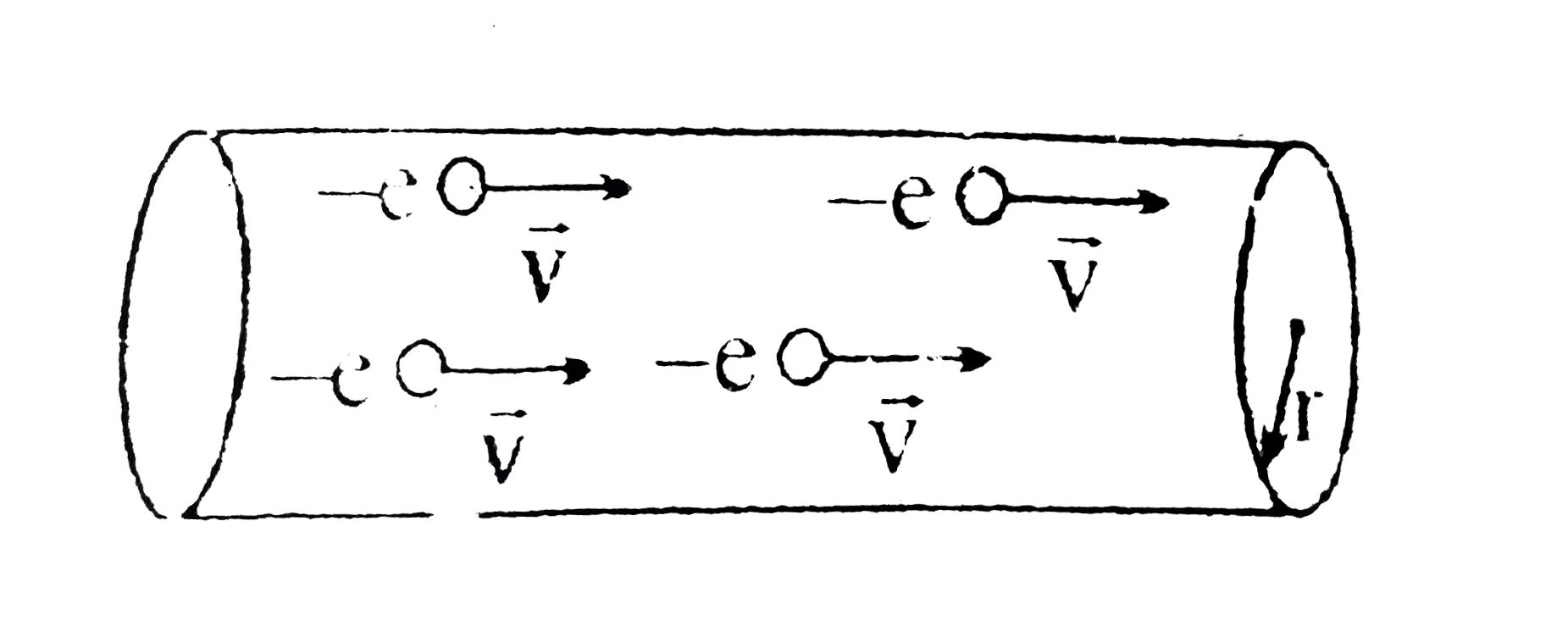
What is net force on the electron at the edge of the beam?
The correct Answer is:B
The total charge inside the cylinder is
Applying Gauss's law gives
The circulation of around the circle is
The position direction for current is along the axis parallel to
The current passing through the circle is
Applying Ampere's law we obtain
The total force acting on an electron is the sum of the electric and magnetic forces

Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Multiple objective131videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Statement-1: The numerical value (n)of a physical quantity is inversely proportional to size of unit (u) being used to measure it.
Statement-2:The magnitude of physical quantity does not change by changing the units.01:23View SolutionThe quantity// quantities that does //do not have mass in its// their dimentions (when we take standard 7 quantities as fundmental) is//are:
05:48View SolutionThe manifestation of band structure in solids is due to
View SolutionA cylinder of height 20m is completely filled with water. The velocity of effux of water (∈ms−1) through a small hole on the side wall of the cylinder near its bottom is
07:49View SolutionHow does the width of the depletion layer of a p-n junction diode change with decrease in reverse bias?
01:38View SolutionA beam of electrons deflects more than a beam of alpha-"particles" in an electric field. Electrons possess negative charge while alpha-"particles" possess positive charge.
03:03View SolutionA beam of electrons has radius r and contains 'n' electrons per cubic meter moving with velocity →v along the beam (figure). Assume that a beam that is much longer than its diameter forms a cylinderically symmetric distribution of charge and current. The beam expands if the electric force exceeds the magnetic force. So long as the expansion is slow, the approximations of cylindrical symmetry and static fields remain valid.
 What is electric field produced on the edge of the beam?03:27View Solution
What is electric field produced on the edge of the beam?03:27View SolutionWhen electron beam passes through an electric field,they gain kinetic energy. If the same beam passes through magnetic field, then
03:43View SolutionA long, narrow beam of electrons, of uniform cross-section consists of electrons moving with velcity v ( c= velocity of light ). The ratio of the electric field to the magnetic field at any point near the beam is
01:37View SolutionAn electron beam enters a magnetic field right angles to it as shown in the Figure. The direction of force acting on the electron beam will be :
04:06View Solutionएक α- किरण पुंज (+X अक्ष ) के अनुदिश प्रक्षेपित किया जाता है। यह एक चुम्बकीय क्षेत्र के कारण +Y अक्ष के अनुदिश बल का अनुभव करता है। चुम्बकीय क्षेत्र की दिशा क्या होगी?
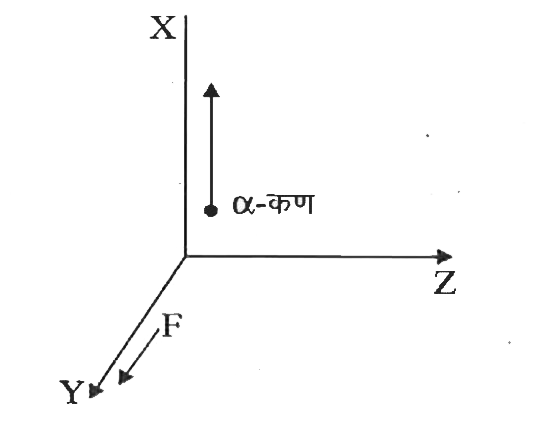 View Solution
View Solutionएक इलेक्ट्रॉन पुंज E तीव्रता के विद्युत क्षेत्र एवं B तीव्रता के चुम्बकीय क्षेत्रों के क्रॉसित क्षेत्र में प्रवेश करता है। इलेक्ट्रॉन की किस चाल के लिए इलेक्ट्रॉन पुंज अविचलित रहेगा।
04:31View SolutionA proton beam is fired from west to east and an electron beam is fired parallel to it in the same direction. Force on the electron beam will be
02:05View SolutionA proton beam is moving along the direction of a magnetic field. What force acts on the proton beam ?
01:37View SolutionAn electron enters a portion of the homogenous electric and magnetic field moving along the beam + y. If the beam passes through this part, the magnetic field B will be the direction of electric field E respectively:
02:00View Solution

