A beam of electrons is moving with uniform velocity in a region having transverse uniform electric and magnetic field of strength. 100 V/m and 0.1 T respectively at right angles to the direction of beam. The velocity of the electrons is
100 m/s
10 m/s
1000 m/s
500 m/s
To solve the problem, we need to find the velocity of the electrons moving in a region with a uniform electric field (E) and a magnetic field (B). The given values are:
- Electric field strength, E = 100 V/m
- Magnetic field strength, B = 0.1 T
1. Understand the Forces Acting on the Electron:
- The electron experiences two forces:
- The electric force (FE) due to the electric field, which acts in the direction of the electric field.
- The magnetic force (FB) due to the magnetic field, which acts perpendicular to both the velocity of the electron and the magnetic field direction.
2. Set Up the Force Balance:
- For the electron to move with uniform velocity, the net force acting on it must be zero. This means the electric force must balance the magnetic force:
FE=FB
3. Write the Expressions for the Forces:
- The electric force is given by:
FE=qE
- The magnetic force is given by:
FB=qvB
- Here, q is the charge of the electron, v is the velocity of the electron, E is the electric field strength, and B is the magnetic field strength.
4. Equate the Forces:
- Setting the two forces equal gives:
qE=qvB
- Since q (the charge of the electron) appears on both sides, we can cancel it out (as long as q≠0):
E=vB
5. Solve for the Velocity (v):
- Rearranging the equation to solve for v:
v=EB
6. Substitute the Given Values:
- Now, substituting the values of E and B:
v=100V/m0.1T=1000.1=1000m/s
7. Final Answer:
- The velocity of the electrons is 1000m/s.
- Magnetic field strength, B = 0.1 T
- The electron experiences two forces:
- The electric force (FE) due to the electric field, which acts in the direction of the electric field.
- The magnetic force (FB) due to the magnetic field, which acts perpendicular to both the velocity of the electron and the magnetic field direction.
- For the electron to move with uniform velocity, the net force acting on it must be zero. This means the electric force must balance the magnetic force:
FE=FB
- The electric force is given by:
FE=qE
- The magnetic force is given by:
FB=qvB
- Here, q is the charge of the electron, v is the velocity of the electron, E is the electric field strength, and B is the magnetic field strength.
- Setting the two forces equal gives:
qE=qvB
- Since q (the charge of the electron) appears on both sides, we can cancel it out (as long as q≠0):
E=vB
- Rearranging the equation to solve for v:
v=EB
- Now, substituting the values of E and B:
v=100V/m0.1T=1000.1=1000m/s
- The velocity of the electrons is 1000m/s.
Topper's Solved these Questions
Similar Questions
A beam of electrons is moving with constant velocity in a region having simultaneous perpendicular electric and magnetic fields of strength 20Vm−1 and 0.5 T, respectively at right angles to the direction of motion of the electrons. Then, to move undeflected the velocity of electrons must be
(a) 8m/s (b) 20m/s (c) 40m/s (d) 140m/s
View SolutionAn electron is fired parallel to uniform electric and uniform magnetic field acting simultaneously and in the same direction. The electron
View Solution
Knowledge Check
If an electron is moving with velocity v produces a magnetic field →B, then
Athe direction of field →B will be same as the direction of velocity →v.Bthe direction of field →B will be opposite to the direction of velocity →v.Cthe direction of field →B will be perpendicular to the direction of velocity →v.Dthe direction of field →B does not depend upon the direction of velocity →v.
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure

View SolutionA small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View SolutionUniform electric and magnetic fields are produced in the same direction. An electron moves in such a way that its velocity remains in the direction of electric field. The electron will-
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
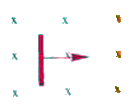
View Solution(A) : An electron moving with uniform velocity enters uniform magnetic field perpendicularly and then a uniform electric field in the same direction. Nature of paths followed by electron in both the fields will be same.
(R) : The force applied by magnetic and electric field on electron are in the same direction.
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
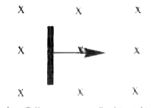
View SolutionA proton and a deuteron having equal momenta enter in a a region of a uniform magnetic field at right angle to the direction of a the field. What is the ratio of their radius of trajectory?
View Solution
