Consider standing wave formed due to superposition of two plane waves having the same amplitude, frequency and moving in opposite direction. Mark the correct statements:
the energy of a standing wave transforms completely into potential energy and at some other instant into kinetic energy during a part of complete cycle.
kinetic energy and potential energy attain their maximum and minimum values simultaneously
there is transition of energy from each node to its adjacent antinodes and back.
the time averaged energy flux in any cross section of the wave is zero.
The correct Answer is:A, C, D
Step by step video, text & image solution for Consider standing wave formed due to superposition of two plane waves having the same amplitude, frequency and moving in opposite direction. Mark the correct statements: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective107videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
Knowledge Check
- Question 1 - Select One
For superposition of two waves, the following is correct
Athey must have the same frequency and wavelengthBthey must have equal frequencies but may have unequal wavelengthsCthey must have the same wave-length, but may have different frequenciesDthey may have different wavelength and different frequencies - Question 2 - Select One
The two waves of same frequency moving in the same direction give rise to
ABeatsBInterferenceCStationary wavesDNone of these - Question 3 - Select One
Consider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Amplitude of simple harmonic motion of a point on the string that is located at x=1.8cm will beA3.3cmB6.7cmC4.9cmD2.6cm
A stationary wave is formed by superposition of two constituent waves, having amplitude, frequency and velocity as 10 cm, 40 Hz and 200 cm/s, respectively. Write the equation of the stationary wave.
View SolutionA travelling wave of amplitude 5A is partically reflected from a bounday with the amplitude 3A. Due to superposition of two waves with different amplitude in opposite direction a standing wave pattern is formed. Datermine the ratio of amplitude at antinode to node.
View SolutionConsider a standing wave formed on a string . It results due to the superposition of two waves travelling in opposite directions . The waves are travelling along the length of the string in the x - direction and displacements of elements on the string are along the y - direction . Individual equations of the two waves can be expressed as
Y1=6(cm)sin[5(rad/cm)x−4(rad/s)t]
Y2=6(cm)sin[5(rad/cm)x+4(rad/s)t] Here x and y are in cm.
Answer the following questions.
Figure 7.104( c) shows the standing wave pattern at t=0 due to superposition of waves given by y1 and y2 in Figs.7.104(a) and (b) . In Fig. 7.104 (c ) , N is a node and A and antinode . At this instant say t=0 , instantaneous velocity of points on the string
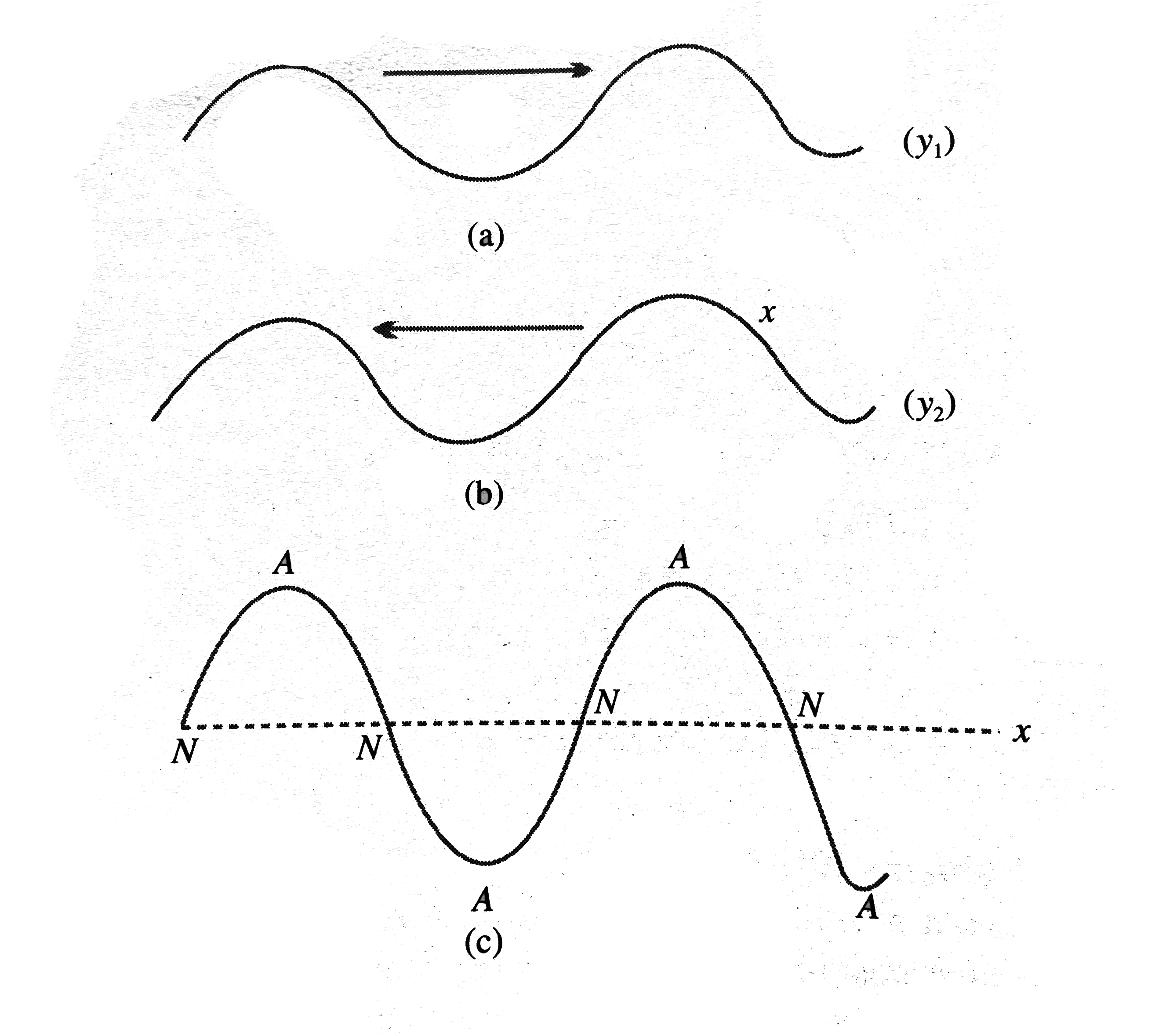 View Solution
View SolutionA standing wave arises on a string when two waves of equal amplitude , frequency and wavelength travelling in opposite superimose. If the frequency of oscillation of the standing waves
View SolutionS1: Sound travel faster in water than in air.
S2: The fundamental frequency of closed organ pipe increases if its diameter is increased.
S3: Beats are created by superposition of two sound waves with the same amplitude moving in same directions with slightly different frequncies.View Solution

