A metal cylinder of mass kg is heated electrically by a 12 W heater in a room at C. The cylinder temperature rises uniformly to C in 5 min and finally becomes constant at C Assuming that the rate of heat losss is proportional to the excees temperature over the surroundings,
the rate of loss of heat of the cylinder to surrounding at C is 2W
the rate of loss of heat of the cylinder to surrounding at C is 12W
the rate of loss of heat of the cylinder to surrounding at C is 5W
the rate of loss of heat of the cylinder to surrounding at C is 30W.
The correct Answer is:A, B
Rate of heat loss
At C Rate of heat loss = Rate of heat supplied =12W
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective107videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
A metal ball of mass 1kg is heated by means of a 20W heater in a room at 20∘C . The temperature of the ball becomes steady at 50∘C . (a) Find the area of loss of heat to the surrounding when the ball is at −50∘C . (b) Assuming Newton's law of cooling, calculate the rate of loss of heat to the surrounding when the ball is at 30∘C . (c) Assume that the temperature of the ball rises uniformly from 20∘C to 30∘C in 5 minutes. Find the total loss of heat to the surrounding during this period. (d) Calculate the speific heat capicity of the metal.
View SolutionA metal ball of 1kg mass is heated by a 20W heater in a room at20∘C. After some time temperature of ball becomes steady at 50'∘C. Find the rate of loss of heat by the ball to surrounding when its temperature becomes 50∘C. Also find the rate at which it looses heat to the surrounding when its temperature was 30∘C.
View Solution
Knowledge Check
- Question 1 - Select One or More
A metal cylinder of mass 0.5kg is heated electrically by a 12W heater in a room at 15∘C The cylinder temperature rises nuniformly to 25∘C in 5 min and finally becomes constant at 45∘C Asuming that the rate of heat loss is proporational to the excess temperature over the surroundings .
AThe rate of loss of heat of the cylinder to surrounding at 20∘C is 2W .BThe rate of loss of heat of the cylinder to surrounding at 45∘C is 2W .CSpecific heat capacity of metal is 240In(3/2)J/kg∘CDNone of these - Question 2 - Select One
A metal ball of mass 2kg is heated means of a 40W heater in a room at 25∘C. The temperature of the ball beomes steady at 60∘C.
Assume that the temperature of the ball rises uniformly from 25∘C to 39∘Cin2 minutes. Find the total loss of heat to the surrounding during this period.A900JB940JC960JD1000J - Question 3 - Select One
A metal ball of mass 2kg is heated means of a 40W heater in a room at 25∘C. The temperature of the ball beomes steady at 60∘C.
Find the rate of loss of heat to the surrounding when the ball is at 60∘C.A40WB16WC96WD100W
A metal bal of mass 1 kg is heated by means of a 20 W heater in a room at 20∘C. The temperature of the ball becomes steady at 50∘C. Assume newton's law of cooling to hold good in the given situation. The temperature of the bal rises uniformly from 20∘C to 30∘C in 5 minutes. select the correct alternatives
(1) The rate of heat loss by ball to surrounding is 20 W, when it is at 50∘
(2) Ther ate of heat loss by ball to surrounding is 203W, when it is at 30∘C
(3) The rate of heat loss by ball to surrounding 20 W, when it is at 30∘C
(4). The specific heat capacity of the gas is 500 J/kg K.View SolutionA metal ball of mass 1.0 kg is kept in a room at 15∘C. It is heated using a heater. The heater supplies heat to the ball at a constant rate of 24 W. The temperature of the ball rises as shown in the graph. Assume that the rate of heat loss from the surface of the ball to the surrounding is proportional to the temperature difference between the ball and the surrounding. Calculate the rate of heat loss from the ball when it was at temperature of 20∘C.
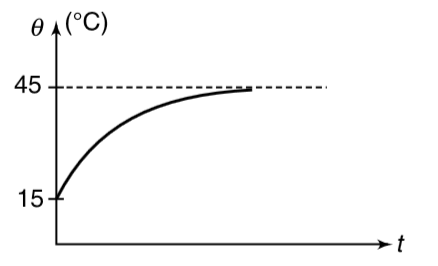 View Solution
View SolutionNewton’s law of cooling says that the rate of cooling of a body is proportional to the temperature difference between the body and its surrounding when the difference in temperature is small.
(a) Will it be reasonable to assume that the rate of heating of a body is proportional to temperature difference between the surrounding and the body (for small difference in temperature) when the body is placed in a surrounding having higher temperature than the body?
(b) Assuming that our assumption made in (a) is correct estimate the time required for a cup of cold coffee to gain temperature from 10∘C to 15∘C when it is kept in a room having temperature 25∘C. It was observed that the temperature of the cup increases from 5∘C to 10∘C in 4 minView SolutionThe temperature of a body falls from 40∘C to 30∘C in 10 min when placed in a surrounding of constant temperature 15∘C. Find the time taken for the temperature of the body to becomes 20∘C
View SolutionA block is kept in a room which is at 20∘C. To raise the temperature of the block, heat is given to it at a constant rate of 600 watt (using an electric heater). The temperature of the block rises with time as shown in the graph. The slope of the graph at time t=0 is 3∘Cs−1. Once the temperature rises to 60∘C, the heater is switched off and another heater is switched on to maintain the temperature of the block at 60∘C. This new heater supplies heat at a constant rate of 100 watt. Assume that heat capacity of the block remains constant for the range of temperature involved.
(a) Explain why the slope of the given graph is decreasing with time.
(b) Calculate the heat capacity of the block.
(c) If the 100 W heater is also switched off, what will be initial rate of cooling of the block?
(d) Assuming that rate of heat loss by the block to the surrounding is proportional to difference in its temperature with surrounding, calculate the heat radiated per second by the block when it was at 30∘C.
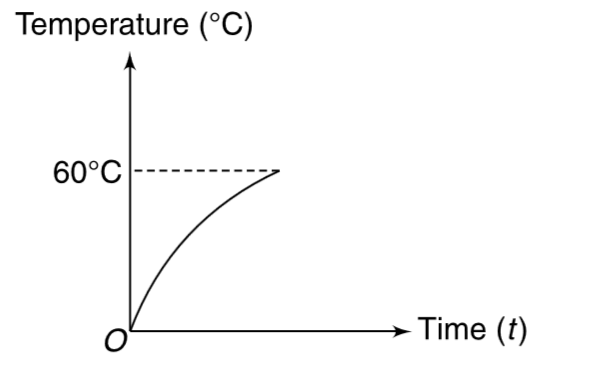 View Solution
View Solution

