In Young's double slit experiment, phase difference between the waves at a point on screen having intensity less than the average intensity on screen may be
π/4
2π/3
π
7π/8
The correct Answer is:B, C, D
Let maximum intensity be I0
I=I0ωtΔϕ2
Iav=I02
I<Iav⇒cos2(Δϕ2)<12
⇒cos(Δϕ2)<1√2
⇒π2<Δϕ<3π2
Topper's Solved these Questions
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Subjective107videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Additional topic70videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - MASTER PRACTICE PROBLEMEXERCISE - Reasoning75videos
MASTER PRACTICE PROBLEM
- BOOK - BANSALCHAPTER - FLUID MECHANICSEXERCISE - PYQS AIEEE10videos
FLUID MECHANICS
- BOOK - BANSALCHAPTER - SEMICONDUCTORSEXERCISE - CBSE Question32videos
SEMICONDUCTORS
Similar Questions
In young's double slit experiment relative intensity at a point on the screen may be defined as ratio of intensity at that point to the maximum intensity on the screen. Light of wavelength 7500∘A A passing through a double slit, produces interference pattern of relative intensity variation as shown in Fig. θ on horizontal axis represents the angular position of a point on the screen
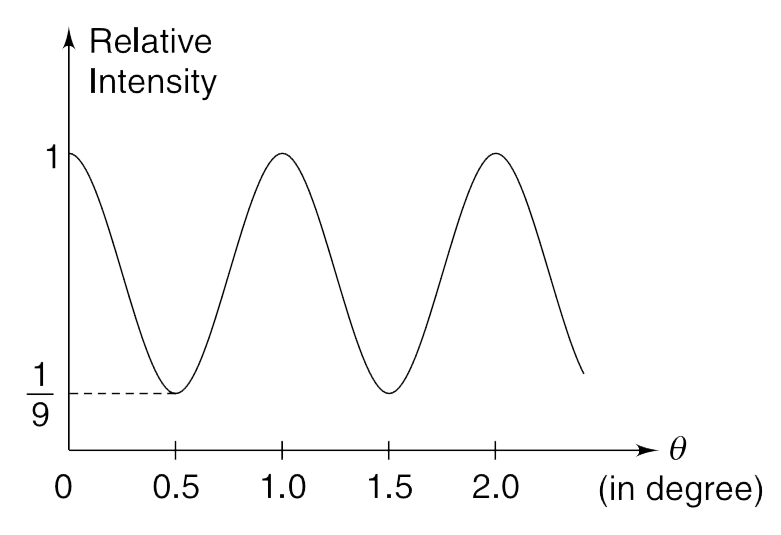
(a) Find separation d between the slits.
(b) Find the ratio of amplitudes of the two waves producing interference pattern on the screen.View SolutionIn Young's double-slit experiment, the path difference between two interfering waves at a point on the screen is 5λ2,λ being wavelength of the light used. The ___________ dark fringe will lie at this point.
View Solution
Knowledge Check
- Question 1 - Select One
In Young's double-slit experiment, the path difference between two interfering waves at a point on the screen is 13.5 times the wavelength. The point is
ABright but not central brightBNeither bright not darkCCentral brightDDark - Question 2 - Select One
In Young's double slit experiment, the phase difference between the two waves reaching at the location of the third dark fringe is
AπB3π2C5πD3π - Question 3 - Select One
In the Young's double slit experiment, if the phase difference between the two waves interfering at a point is ϕ, the intensity at that point can be expressed by the expression
A(a) I=√A2+B2cos2φB(b) I=ABcosφC(c)I=A+Bcosφ2D(d) I=A+Bcosφ
In Young's double slit experiment the phase difference between the waves reaching the central fringe and fourth bright fringe will be
View SolutionIn a Young's double slit experiment, the central point on the screen is
View SolutionIntensities of light due to the two slits of Young's double-slit experiment are I and 4I. How far from the centre maxima will the intensity be equal to the average intensity on the screen? (β is the fringe width.)
View SolutionIn Young's double-sit experiment, if the superimposing waves have amplitude a0 and intensity I0, then the average intensity of the light in te fringe pattern formed on a screen will be
View SolutionIn Youngsdoub≤slitexperiment,thephased⇔erentbetweentwocoherentsourcesofequal∫ensityisπ3.The∫ensityatap∮whichisatequaldistanceomthetwoslitsis(l_@) is maximum intensity)
View Solution

