Column-I describe the value of variables indicated in column-II Assume potential energy in gravitation and electrostatics to be zero at infinity if the quantity mentioned in columnII is a vector positive and negative refer to the direction and increasing or decreasing refer to magnitude Match the appropriate entries.
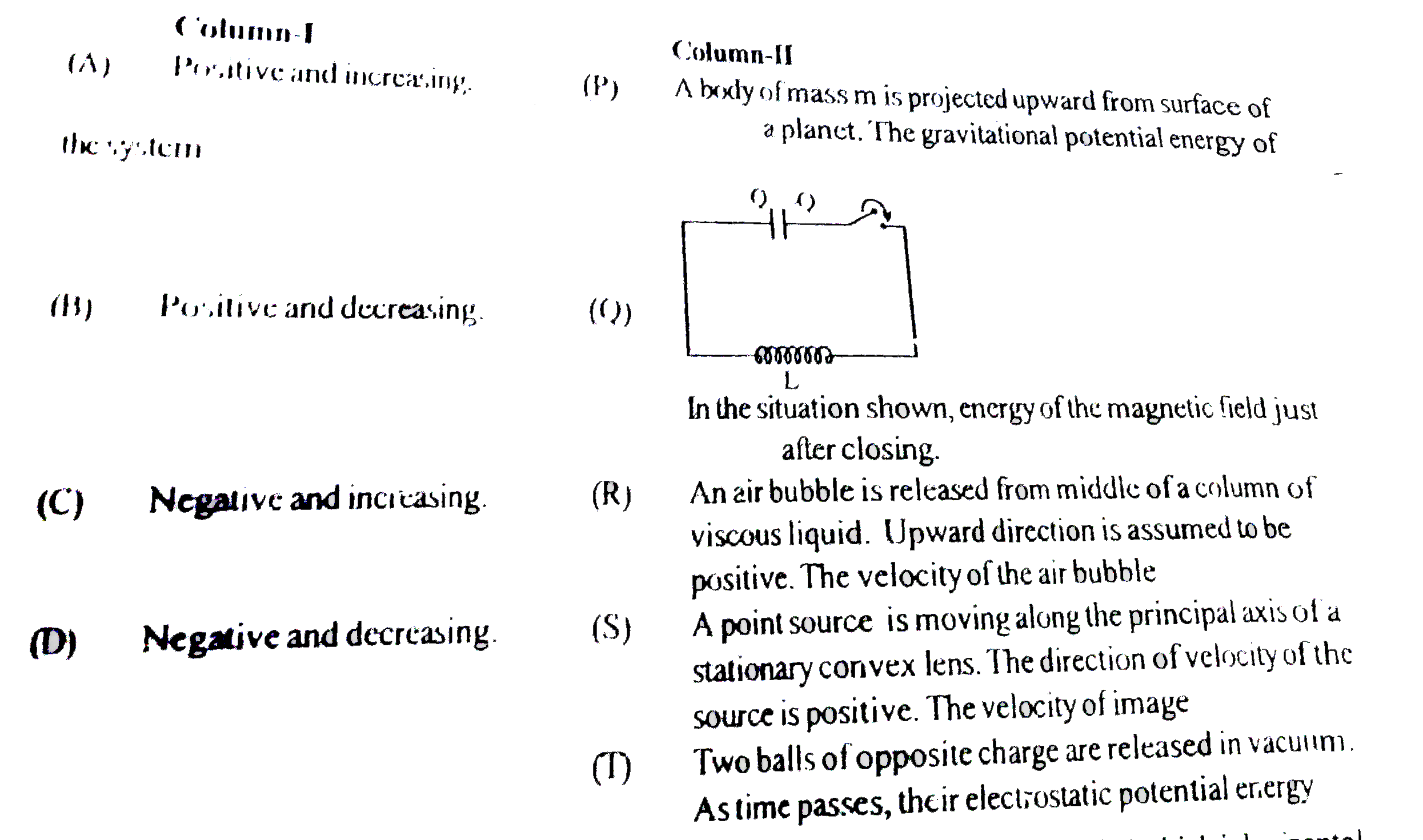
The correct Answer is:[(A)QRS(B)S(C)P(D)T]
(P) U=−Gm1m2r -ve and increasing
(Q) q⏐↓⇒Ucap↑⏐⇒Umg↑⏐ +ve and increasing
(R) v↑and∈creases
(S) If object is from Y to 2fV1↓
If object is from 2f to fV1↑ velocity is always in same direction
(T) U=−kQqrr⏐⏐
⏐↓becomesmore−ve
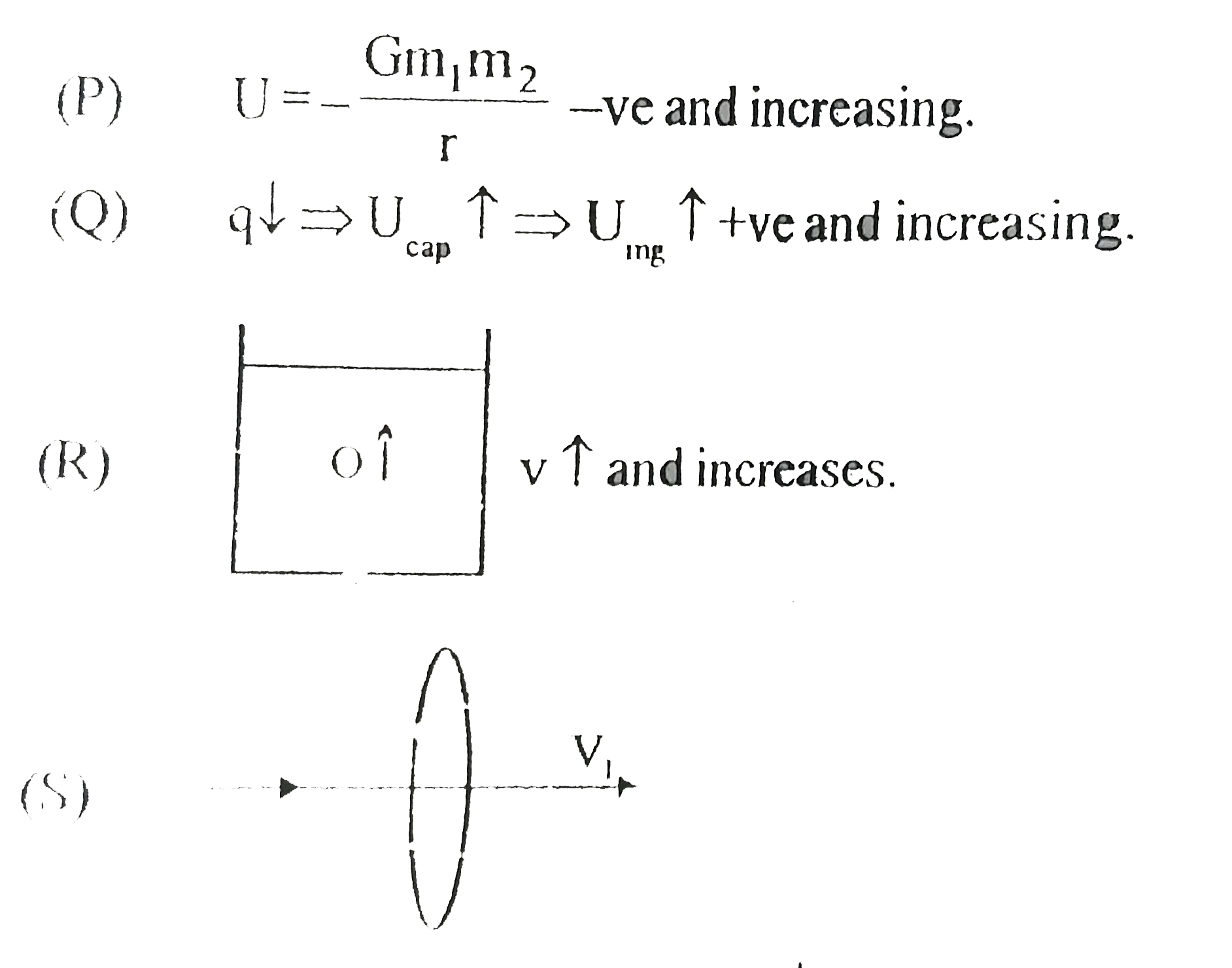
Topper's Solved these Questions
Similar Questions
In column - I some physical situations are mentioned, in column - II corresponding variations of resultant quantities percentasge errors are mentioned. Match column - I entries appropriately with column - II entries

View SolutionIf α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in
Column-I to their values in column-II :
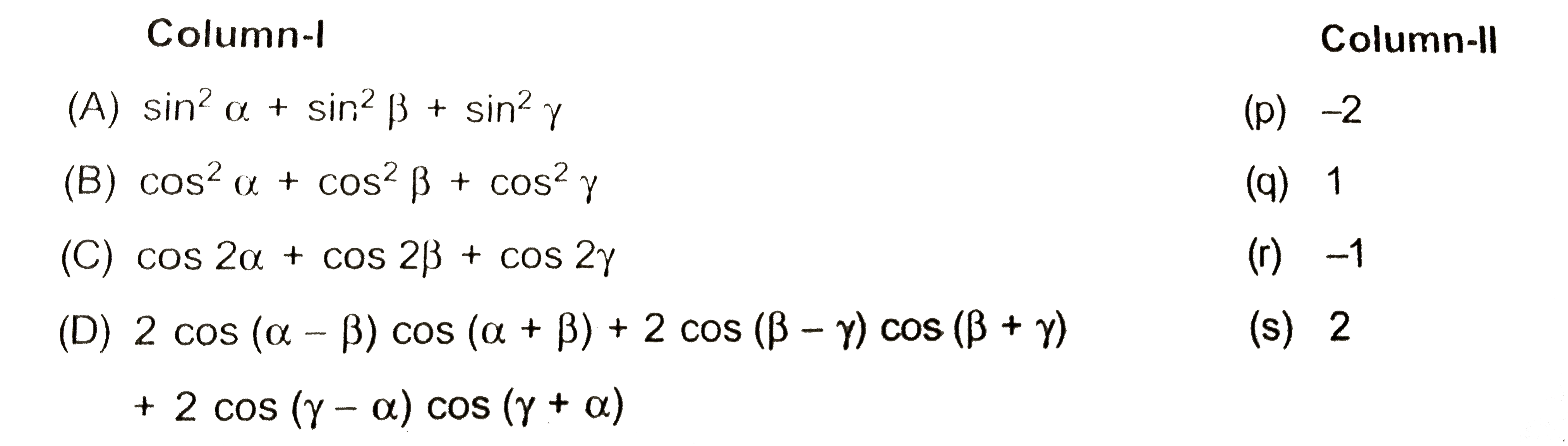
View Solution
Knowledge Check
A cubical block of mass m and surface area 6A is placed on a thick layer of viscous liquid, of thickness d as shown

Initially the block is at rest. A constant horizontal force F0 starts acting on the block at t = 0. In column - 1 a physical quantity regarding the motion of the block is given and in column-2 corresponding variation with time is given. Match the proper entries from column-2 to column-1 using the codes given below the columns.
Column-IColumn-II(P) X (distance travel by the block as function of time.) (1)αe−βt(α,β≠0)(Q) V (velocity of block as as function of time.)(2)α+βt+γe−δt(α,β,γ,δ≠0)(R) A (acceleration of block as as function of time.)(3)αe−βt−γe−δt(α,β,γ,δ≠0)(S) dK/ dt (rate of change in kinetic energy of block as as function of time.)(4)α+βeγt(α,β,γ≠0)
(here α,β,γ,δ may have different values in each of options)APQRS(A)2134BPQRS(B)2413CPQRS(C)2431DPQRS(D)1243In each situation of column-I, some charge distributions are given with all details explained. In column -II The electrostatic potential energy and its nature is given situation in column -II. Match the proper entries from column-2 to column-1 using the codes given below the columns, Column-I
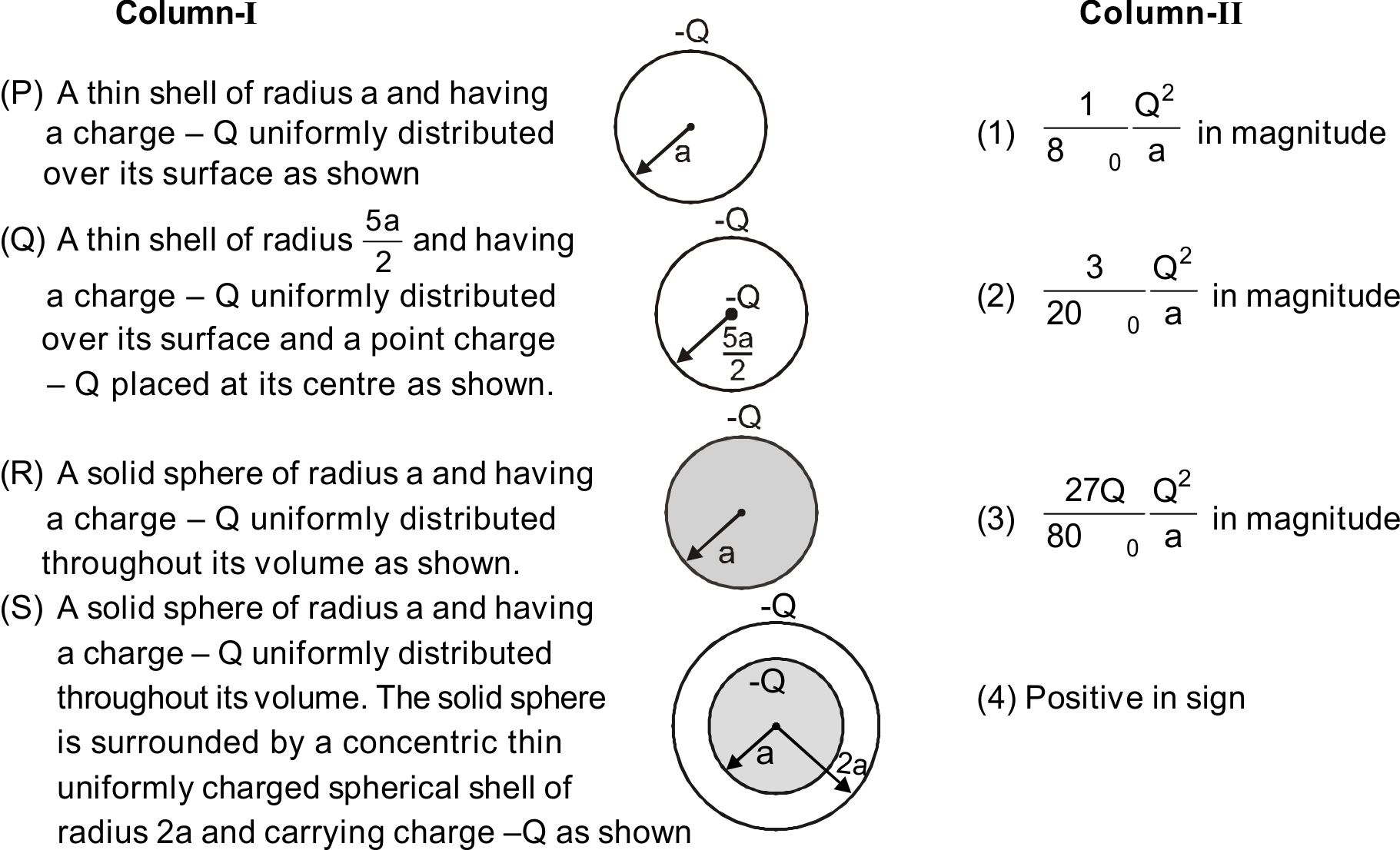 APQRS1243BPQRS4123CPQRS1234DPQRS2431
APQRS1243BPQRS4123CPQRS1234DPQRS2431The potential energy at a point, relative to the reference point is always defined as the negative of work done by the force as the object moves from the reference point to the point considered. The value of potential energy at the reference point itself can be set equal to zero because we are always concerned only with differences of potential energy between two points and the associated change of kinetic energy. A particles A is fixed at origin of a fixed coordinate system. A particle B which is free to move experiences an force →F=(−2ar3+βr2)ˆr due to particle A where ˆr is the position vector of particle B relative to A. It is given that the force is conservative in nature and _potential energy at infinity is zero. If B has to be removed from the influence of A, energy has to be supplied for such a process. The ionization energy E 0 is work that has to be done by an external agent to move the particle from a distance r0 to infinity slowly. Here r0 is the equilibrium position of the particle
What is potential energy function of particle as function of r.Aαr2−βrB−αr2+βrC−αr2−βrDαr2+βr
If α,β,γ are the angles which a line makes with positive direction of the axes, then match the quantities in column-I to their values in column-II:
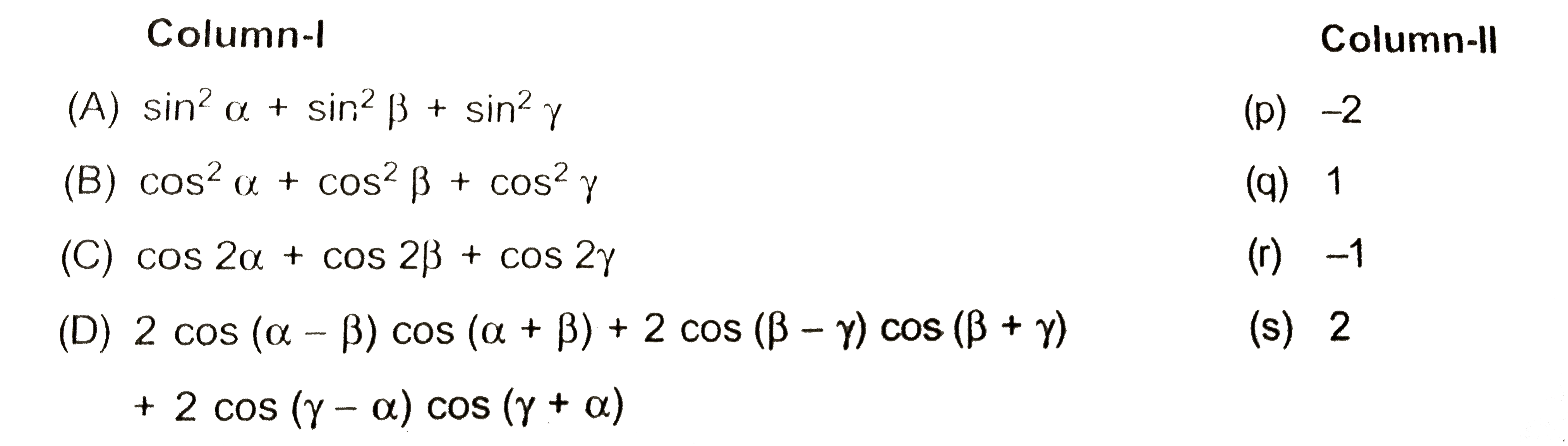
View SolutionIn the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.
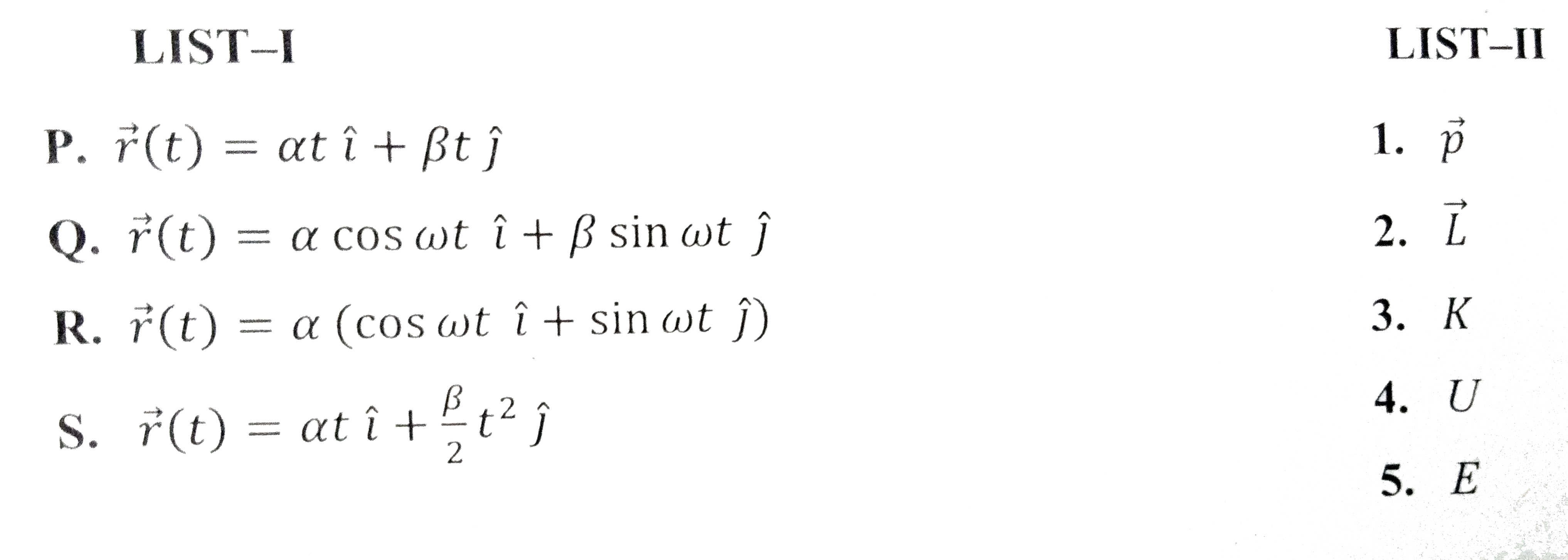
View SolutionThe circuit involves two ideal cells connected to a 1μF capacitor via a key K. Initially the key K is in position 1 and the capacitor is charged fully by 2V cell. The key is then pushed to position 2. Column I gives physical quantities involving the circuit after the key is pushed from position 1. Column II gives corresponding results. Match the statements in Column I with the corresponding values in Column II.
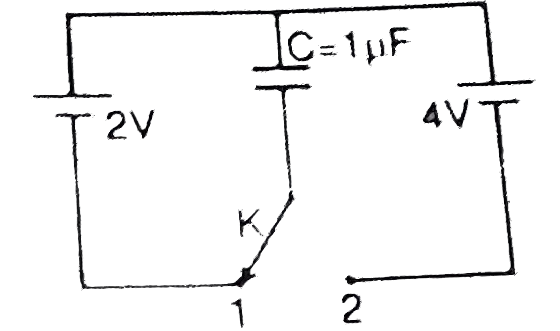
Column I Column II(A) The net charge crossing the 4 volt cell in μC is(p) 2(B) The magnitude of work done by 4 Volt cell in μJ is(q) 6(C) The gain in potential energy of capacitor in μJ is (r) 8(D) The net heat produced in circuit in μJ is (s) 16
View SolutionThe potential energy at a point, relative to the reference point is always defined as the negative of work done by the force as the object moves from the reference point to the point considered. The value of potential energy at the reference point itself can be set equal to zero because we are always concerned only with differences of potential energy between two points and the associated change of kinetic energy. A particles A is fixed at origin of a fixed coordinate system. A particle B which is free to move experiences an force →F=(−2ar3+βr2)ˆr due to particle A where ˆr is the position vector of particle B relative to A. It is given that the force is conservative in nature and _potential energy at infinity is zero. If B has to be removed from the influence of A, energy has to be supplied for such a process. The ionization energy E 0 is work that has to be done by an external agent to move the particle from a distance r0 to infinity slowly. Here r0 is the equilibrium position of the particle
Find the ionization energy E0 of the particle B
View SolutionThe potential energy at a point, relative to the reference point is always defined as the negative of work done by the force as the object moves from the reference point to the point considered. The value of potential energy at the reference point itself can be set equal to zero because we are always concerned only with differences of potential energy between two points and the associated change of kinetic energy. A particles A is fixed at origin of a fixed coordinate system. A particle B which is free to move experiences an force →F=(−2ar3+βr2)ˆr due to particle A where ˆr is the position vector of particle B relative to A. It is given that the force is conservative in nature and _potential energy at infinity is zero. If B has to be removed from the influence of A, energy has to be supplied for such a process. The ionization energy E 0 is work that has to be done by an external agent to move the particle from a distance r0 to infinity slowly. Here r0 is the equilibrium position of the particle
If particle B is transferred slowly from point P1(√2r0,√2r0) to point P2(r0√2,r0√2) in the xy-plane by an external agent, calculate work required to be done by it in the process:
View Solution
