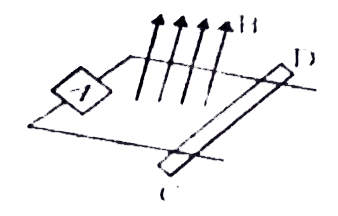
A homogeneous magnetic field B is perpendicular to a sufficiently long trach of width l which is horizontal A frictionless conducting resistanceless rod of mass m stradless the two rails of the track as shown in the figure. Entire arrangement lies in horizontal plane. For the situation suggested in column-II match the appropriate entries in column-I the rails are also resistancesless.


The correct Answer is:[(A)PQ;(B)PQ;(C)R;(D)PST]
(A) V−BlvR=i
F=V−BlvR×Bl
(B) ilB=ma⇒lBdQdt=mdvdt⇒BlQm
Ui>Uf because energy is dissipated in em radiator
(C) No energy dissipated as no resistance R rightarrow Red executes SHM
F=ilB→≤ft⇒fext→right
F=ilBLdidt=Blv⇒ not possible to move with constant v
Topper's Solved these Questions
Similar Questions
A homogeneous magnetic field B is perpendicular to a sufficiently long fixed track of width l which is horizontal. A frictionless rod of mass m straddles the two rail of the track as shown in the figure. Entir arrangement lies in horizontal plane. For the situation suggested in column-II match the appropriate entries in column-II. The rails are also resistanceless.

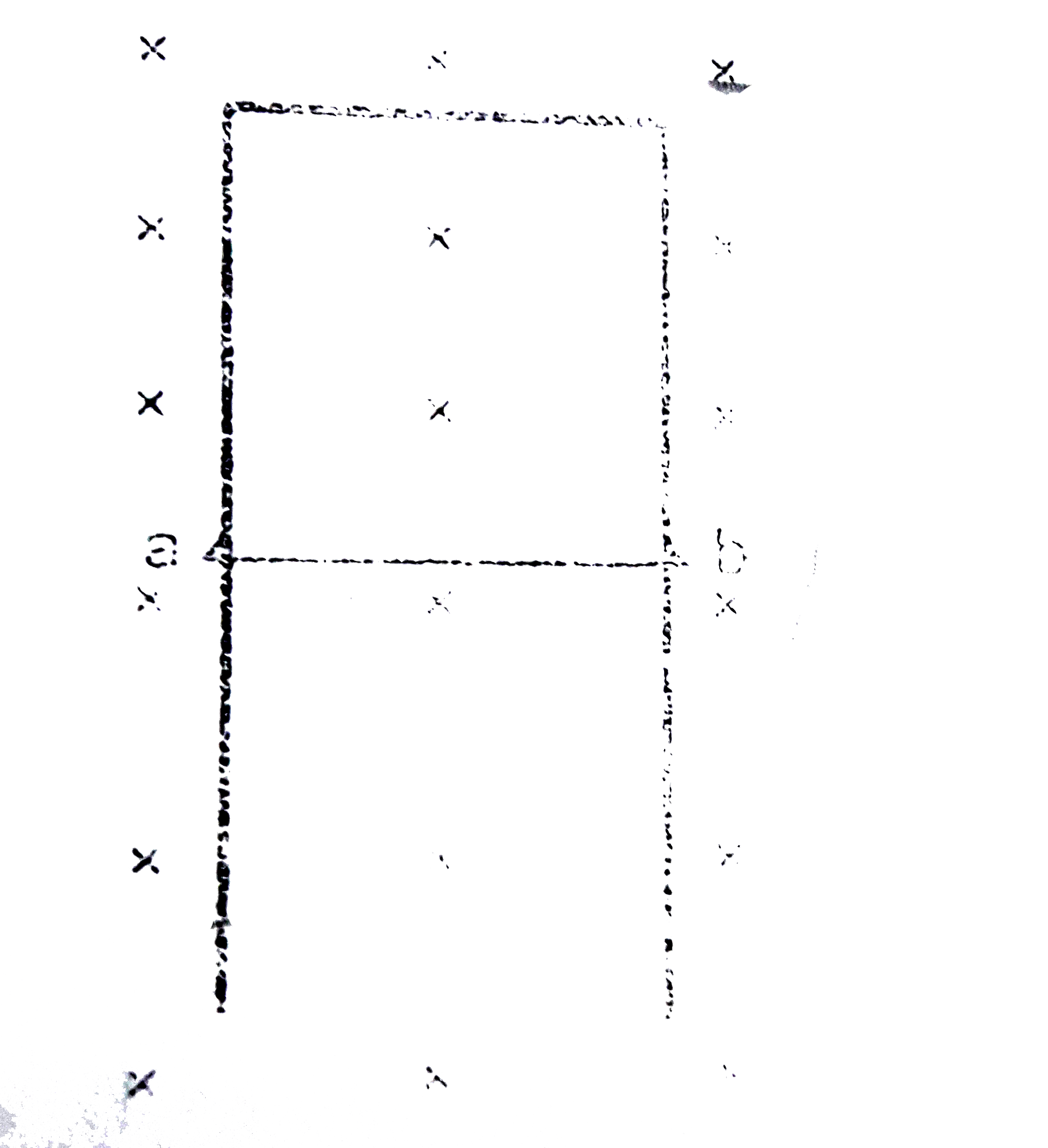
View SolutionA copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
View Solution
Knowledge Check
A copper wire ab of length l, resistance r and mass m starts sliding at t=0 down a smooth, vertical, thick pair of connected condcuting rails as shown in figure.A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct.
 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrv.CThe velocity of the wire as a function of time vm(1−e−gt/vm)(where vm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm)(where vm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrv.CThe velocity of the wire as a function of time vm(1−e−gt/vm)(where vm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm)(where vm=mgrB2l2)A wire ab of length l, mass m and resistance R slides on a smooth thick pair of metallic rails joined at the bottom as shown in fig. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exist in the region. If the wire slides on the rails at a constant speed v, then the value of B is -
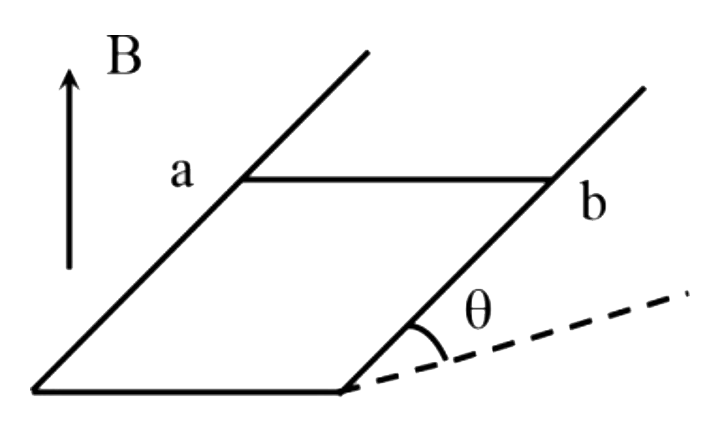 A√mgRvl2cos2θB√mgRcosθvl2sin2θC√mgRv2l2sin2θD√mgRsinθvl2cos2θ
A√mgRvl2cos2θB√mgRcosθvl2sin2θC√mgRv2l2sin2θD√mgRsinθvl2cos2θA copper wire ab of length l, resistance r and mass m start sliding at t=0 down a smooth, vertical, thick pair of connected conducting rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails which options are correct .
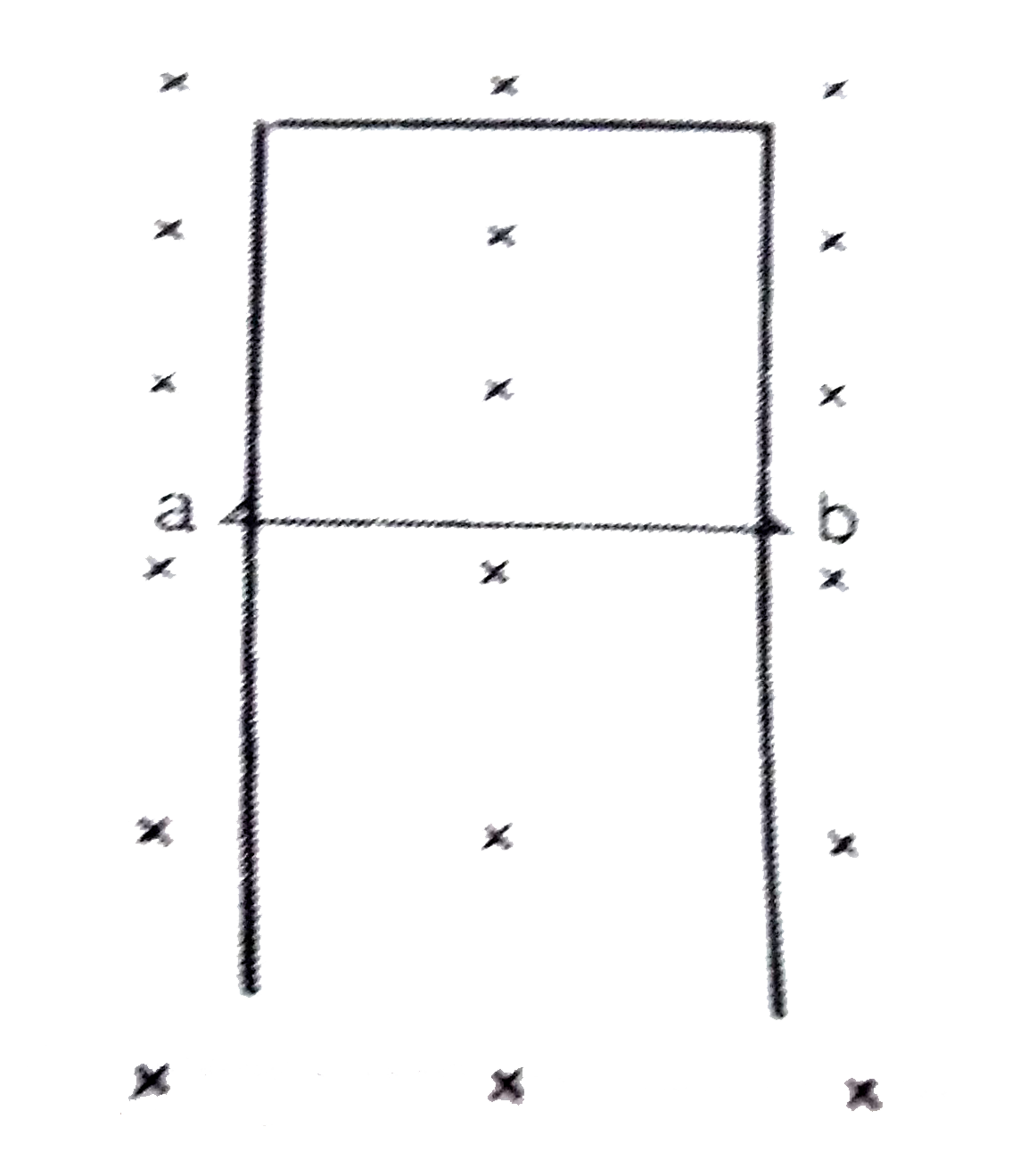 AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
AThe magnitude and direction of the induced current in the wire when speed of the wire v is vBlr, a to bBThe downward acceleration of the wire at this instant g−B2l2mrvCThe velocity of the wire as a function of time vm(1−e−gt/vm),(wherevm=mgrB2l2)DThe displacement of the wire as a function of time vmt−v2mg(1−e−gt/vm),(wherevm=mgrB2l2)
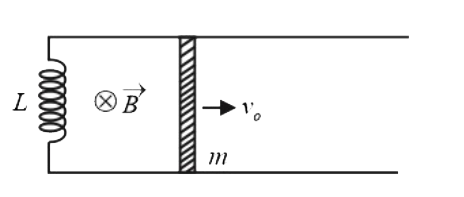
As shown in figure, the two parallel conducting rails, in a horizontal plane, are connected at one end by an inductor of inductance L. A slider (metallic) of mass m, is imparted a Velocity v0, upon the rails, as shown in figure. The period of oscillation of the conducting rod is
View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View SolutionAs shown in figure, the two parallel conducting rails, in a horizontal plane, are connected at one end by an inductor of inductance L. A slider (metallic) of mass m, is imparted a Velocity v0, upon the rails, as shown in figure. The period of oscillation of the conducting rod is

View SolutionA conducting wire xy of lentgh l and mass m is sliding without friction on vertical conduction rails ab and cd as shown in figure. A uniform magnetic field B exists perpendicular to the plane of the rails, x moves with a constant velocity of

View Solution
